Zadani uloh

Uvod
Problem A - Hyperoxni hypergony
Problem B - Prunik hyperkvadru
Problem C - Posadka
Problem D - Kolonie
Problem E - Vyplneni prostoru
Problem F - Prstencove generatory
Problem G - Optimalni trasa
Problem H - Posloupnost planet

Uvod

Pise se rok 2047. Nejvyznamejsi udalosti letosniho roku bude bezesporu start hyperprostorove kosmicke lodi Nostromo na vyzkumnou vypravu ke vzdalenym galaxiim. Kosmicka lod Nostromo je prvni hyperprostorova kosmicka lod vyrobena na planete Zemi. Stavbe teto lodi predchazelo mnoho let teoretickych vyzkumu a praktickych experimentu. Nostromo je vysledkem neunavne prace stovek fyziku, matematiku, konstrukteru, pocitacovych specialistu a mnoha dalsich odborniku.

Material, ktery se vam prave dostal do ruky, popularni formou priblizuje nektere problemy, se kterymi se museli tvurci kosmicke lodi Nostromo potykat.

Problem A

Hyperoxni hypergony

V souvislosti s konstrukci nove hyperkosmicke lodi bylo pochopitelne nutne rozsirit celou radu stavajicich vedeckych disciplin a zalozit nekolik zcela novych. Kuprikladu jednim z fundamentalnich problemu aplikovane hypermaticke hypermetrie, ktery ma radu praktickych aplikaci zejmena pri navrhu umisteni hyperlacnich hyperuzic slouzicich ke komunikaci hyperkosmicke lodi se Zemi pomoci hypervln, je problem hyperoxnosti hypergonu. Tento problem byl teoreticky popsan teprve nedavno, ale vzhledem k tomu, ze na jeho reseni zavisi mnoho konstrukcnich rozhodnuti stavitelu hyperkosmicke lodi, je nutne co nejrychleji najit efektivni algoritmus pro jeho reseni. Jelikoz se jedna o problematiku ve vedeckych kruzich znamou, muze ted vetsina z vas prejit rovnou na bod ‘Specifikace vstupu’. Pro jistotu zde vsak strucne zopakujeme potrebne zakladni pojmy z hypermaticke hypermetrie:

Mnozinu vsech usporadanych k-tic realnych cisel nazyvame k-hyperostor. Jednotlive prvky k-hyperostoru jsou k-hypery. k je prirozene cislo a nazyvame ho hyperzi.

Nad k-hypery definujeme operaci scitani:

a+b = (a₁, a₂, ...,a_k) + (b₁, b₂, ...,b_k) = (a₁ + b₁, a₂ + b₂, ..., a_k + b_k)

Definujeme rovnez operaci nasobeni k-hyperu realnym cislem:

xa = xa(a₁, a₂, ..., a_k) = (xa₁, xa₂, ..., xa_k)

Definujeme zobrazeni zvane hypernost z mnozniny vsech dvojic k-hyperu do mnoziny realnych cisel nasledujicim vztahem:

h(a,b) = SQRT((a₁ - b₁)² + (a₂ - b₂)² + ... + (a_k - b_k)²)

Rekneme, ze k-hyper y je hyperaci k-hyperu x₁, x₂, ...,x_n, pokud existuji realne konstanty a₁, a₂, ..., a_n takove, ze y = a₁x₁ + a₂x₂ + ... + a_nx_n

Mejme danu mnozinu k-hyperu g₁, g₂, ... g_l, ktere nazyvame hyperatory, takovou, ze zadny z hyperatoru neni hyperaci ostatnich. Pak mnozinu vsech k-hyperu, ktere jsou hyperacemi hyperatoru nazyvame l-hypostor. Vsimnete si, ze k-hyperostor je rovnez k-hypostorem.

Hyperoli o polomeru r k-hyperu x (znacime d(x,r)) vzhledem k danemu l-hypostoru H je mnozina vsech k-hyperu y z H, takovych, ze h(x,y) < r .

Hypertrek resp. hypersek podmnoziny P l-hypostoru H vzhledem k H je mnozina vsech takovych k-hyperu y z H, ze pro ne existuje realne r tak, aby hyperoli d(y,r) vzhledem k H bylo podmnozinou P resp. H-P. Mnozinu vsech k-hyperu z P, ktere nepatri ani do hypertrku, ani do hypersku P pak nazyvame hyperanici P.

Podmnozinu Q k-hyperostoru nazyvame hypervislou, pokud pro kazde dva k-hypery x, y z Q existuje posloupnost k-hyperu l₁, l₂, ... , l_n takova, ze l₁ = x, l_n = y a pro vsechna realna a, 0 <= a <= 1, a vsechna prirozena i, i < n, plati, ze al_i +(1 - a) l_i+1 je prvkem Q.

Hypervislou podmnozinu R l-hyperostoru H nazyvame hyperlasti, pokud hypernost libovolnych dvojic z R je shora omezena, R je sjednocenim hypertrku R a hyperanice R a navic je hyperanice R hypervisla. Hyperlast S, podmnozinu l-hypostoru H nazyvame l-hypergonem, pokud bud l = 0 a S obsahuje jen jediny k-hyper nebo pokud l>0 a plati nasledujici podminky:

Neexistuje (l-1)-hypostor obsahujici S.
Existuji (l-1)-hypergony M₁, M₂, ..., M_q takove,ze :
- sjednoceni vsech M_i je hyperanice S
- pro vsechna i, j, i ruzne od j je M_i prunik s M_j bud prazdnou mnozinou a nebo podmnozinou hyperanice M_i a neexistuje takovy (l-1) hypostor J, aby M_i byla podmnozinou J a M_j podmnozinou J

Hypostory M1 az Mq nazyvame hyperanami.

Konecne hyperoxni hypergon S je takovy, kdy pro kazde dva k-hypery x,y z S plati, ze pro vsechna realna a, 0 <= a <= 1, ax + (1-a)y nalezi S.

Vasim ukolem je navrhnout algoritmus, ktery pro dany (k-1)-hypergon z k-hyperostoru zjisti, zda je hyperoxni.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Prvnim radek kazdeho zadani obsahuje prirozene cislo K oznacujici hyperzi hyperostoru, v nemz budeme pracovat. 1 < K <= 10. Pak nasleduje K podbloku, kazdy popisujici hypergony hyperze 0 az K-1.

Prvni podblok, popisujici 0-hypergony, tedy K-hypery, zacina radkem obsahujicim prirozene cislo L reprezentujici pocet 0-hypergonu v rozsahu 3 az 1000. Pak nasleduje L radku kazdy obsahujici K celych cisel v rozsahu -10000 az +10000 reprezentujici kazdy slozky jednotlivych K-hyperu. Pro ucely pozdejsich odkazu oznacime K-hypery po rade cisly 1 az L. To je konec prvniho podbloku.

Dalsich K-1 podbloku ma podobnou strukturu. m-ty podblok popisujici m-hypergony zacina radkem obsahujicim jejich pocet L (coz je prirozene cislo od 3 do 1000). Dale kazdy z nasledujicich L radku obsahuje popis jednoho m-hypergonu. Kazdy zacina prirozenym cislem Q v rozsahu 2 az 100, coz je pocet hyperan a pokracuje Q indexy, coz jsou poradova cisla tech (m-1)-hypergonu, ktere jsou hyperanami prave popisovaneho m-hypergonu.

Posledni, K-ty podblok popisuje vzdy jen jeden (L = 1) (K-1)-hypergon, ktery je treba analyzovat. Muzete predpokladat, ze vstupni data popisuji vzdy hypergon dle vyse uvedene definice.

Ne vsechny hypergony nizsi urovne musi byt pouzity pri popisu hypergonu vyssi urovne. Poradi hyperan neni urceno.

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je slovo ‘Ano’, pokud je dany hypergon hyperoxni nebo slovo ‘Ne’, pokud hyperoxni neni.

Priklad vstupu

Pro vyssi srozumitelnost je priklad vstupu doplnen komentari, ktere se ve skutecnem vstupu nevyskytuji.

3	tri zadani
2	K
3	pocet 0-hypergonu
0 0	slozky 0-hypergonu
1 0
0 1
3	pocet 1-hypergonu
2 1 2	pocet hyperan a indexy do seznamu 0-hypergonu
2 2 3
2 3 1
1	pocet 2-hypergonu, vzdy jen jeden
3 1 2 3	pocet hyperan a indexy do seznamu 1-hypergonu 
2	K pro druhe zadani
4	pocet 0-hypergonu
10 -5	slozky 0-hypergonu
 0 5
-10 -5
0 0
4	pocet 1-hypergonu
2 1 2	pocet hyperan a indexy do seznamu 0-hypergonu
2 2 3
2 3 4
2 4 1
1	pocet 2-hypergonu ... vzdy jen jeden
4 1 2 3 4	pocet hyperan a indexy do seznamu 1-hypergonu
3	K pro treti zadani
8	pocet 0-hypergonu
0 0 0	slozky 0-hypergonu
1 0 0
1 0 1 
0 0 1
0 1 0
1 1 0
1 1 1
0 1 1
12	pocet 1-hypergonu
2 1 2	pocet hyperan a indexy do seznamu 0-hypergonu
2 2 3
2 3 4
2 4 1
2 5 6
2 6 7
2 7 8
2 8 5
2 1 5
2 2 6
2 3 7
2 4 8
6	pocet 2-hypergonu
4 1 2 3 4	pocet hyperan a indexy do seznamu 1-hypergonu
4 5 6 7 8
4 1 10 5 9
4 2 11 6 10
4 3 11 7 12
4 4 9 8 12
1	jen jeden 3-hypergon
6 1 2 3 4 5 6	pocet hyperan a indexy do seznamu 2-hypergonu

Priklad vystupu

Ano
Ne
Ano

Problem B

Prunik hyperkvadru

Jak jiz bylo receno, pri konstrukci hyperkosmicke lodi je nutne vyuzit mnoha novych teoretickych poznatku, zejmena z oblasti hypermetrie. Jednim z mnoha oboru, ktere tezi z poznatku hypermetrie, je take navigace a konstrukce navigacnich systemu. Dulezitou soucasti navigacniho systemu hyperkosmicke lodi Nostromo je jeho cast, ktera vypocitava objem pruniku hyperprostorovych kvadru, jejichz hrany jsou rovnobezne s hranami pravouhleho souradneho systemu.

Vasim ukolem je napsat takovy program.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Na prvnim radku zadani jsou uvedena dve cela cisla D a T oddelena mezerou, 2 <= D <= 1000000, 1 <= T <= 1000000. D je dimenze hyperkvadru, T je pocet jednotlivych hyperkvadru. Dale nasleduje T radku. Kazdy z techto T radku obsahuje 2D celych cisel. Kazda dvojice omezuje velikost hyperkvadru v jednom rozmeru, tj. X_min X_max Y_min Y_max Z_min Z_max...

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je prave jedno cele cislo V - objem pruniku vsech zadanych hyperkvadru.

Priklad vstupu

2
2 3
1 4 1 10
5 8 1 10
3 6 1 2
3 2
1 10 1 10 1 10
1 10 9 11 1 9

Priklad vystupu

0
72

Problem C

Posadka

Pri planovani rozsahle vypravy hyperkosmicke lodi, jakou je Nostromo, je nutne venovat velkou peci tez sestaveni vhodne posadky. Kazdy z clenu vypravy ma ruznou uroven znalosti v ruznych oblastech pruzkumu vesmiru a tudiz ma i pro ruzne oblasti ruznou hodnost. Jeden a tentyz clen vypravy muze byt zaroven kapitanem pro navigaci a desatnikem pro styk s mimozemskymi civilizacemi. S ohledem na stabilitu posadky je nutne, aby posadka byla sestavena hierarchicky, tj. aby zadni dva clenove posadky si nebyli navzajem nadrizeni v ruznych oborech.

Vasim ukolem je napsat program, ktery pro danou sestavu posadky urci, je-li tato sestavena dobre ci spatne.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani zacina radkem obsahujicim prirozene cislo X, 1 <= X <= 500, ktere udava pocet clenu posadky. Kazdy clen posadky ma prideleno osobni cislo. Osobni cisla jsou pridelena souvisle pocinaje cislem 1. Na dalsich radcich zadani nasleduje popis pro kazdeho clena posadky, tedy celkem X popisu. Popis clena s osobnim cislem i je i-ta dvojice radku. Na prvnim radku z kazde dvojice je pocet osobnich cisel, ktera jsou uvedena na druhem radku. Na druhem radku jsou osobni cisla jeho primych nadrizenych pro ruzne obory oddelena mezerou. Osobni cisla primych nadrizenych se mohou opakovat. Cislo i se zde nevyskytne - tedy zadny clen posadky neni primo nadrizen sam sobe.

Specifikace vystupu

Rekneme, ze A je nadrizeny osobe B, jestlize A je primo nadrizeny osobe B nebo existuje osoba C takova, ze A je primo nadrizeny osobe C a zaroven C je nadrizeny osobe B. Za spatne navrzenou posadku povazujeme takovou posadku, kde v posadce existuji takove osoby A a B, ze osoba A je nadrizena osobe B v nekterem oboru a zaroven osoba B je nadrizena osobe A v jinem oboru. Pro kazde zadani musi vystup obsahovat prave jeden radek s textem 'Posadka je navrzena spatne.', pokud je spatne navrzena, jinak s textem 'Posadka je navrzena dobre.'

Priklad vstupu

Priklad vystupu

Posadka je navrzena dobre.
Posadka je navrzena dobre.
Posadka je navrzena spatne.

Problem D

Kolonie

Dulezitym ukolem vypravy hyperkosmicke lodi Nostromo na jeji ceste je zalozeni trvale zakladny na obezne draze planety MX8-26B v souhvezdi Kentaura. Pro tyto ucely ma posadka k dispozici celky slozene z koji s podstavou ve tvaru sestiuhelniku. Vsechny koje jsou konstruovany stejnym zpusobem: V kazde ze sesti stran koje je otvor, ktery slouzi jako pruchod do sousedni koje v pripade, ze je touto stranou smontovana s jinou koji, nebo jako okno do mezihvezdneho prostoru, kdyz je tato strana vnejsi stenou zakladny. Kazdy celek muze byt slozen z jednotlivych koji libovolnym zpusobem. Vyprava ma k dispozici urcity pocet typu takovychto celku a od kazdeho typu urcity pocet kusu. V kazde koji ve vysledne zakladne muze byt ubytovano tolik lidi, kolik ma tato koje oken do mezihvezdneho prostoru.

Vasim ukolem je napsat program, ktery z popisu jednotlivych typu celku a z jejich poctu dokaze urcit, je-li mozne sestavit zakladnu pro dany pocet lidi.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Na prvnim radku zadani jsou uvedena dve prirozena cisla P a T oddelena mezerou, kde P je pocet lidi, pro ktere ma byt postavena zakladna a T pocet typu celku, ktere ma vyprava k dispozici. Dale nasleduje T radku. Na kazdem z techto T radku jsou uvedena dve prirozena C, S a dale S dvojic prirozenych cisel. Vsechna cisla na radku jsou oddelena mezerou. C je pocet celku, ktere ma vyprava od daneho typu celku k dispozici. S je pocet koji, ze kterych je dany typ celku slozen. Popsany celek je vzdy souvisly. Dany celek je popsan souradnicemi stredu podstav koji v souradnem systemu x, y. Kazda dvojice cisel nasledujici za cislem S je souradnice stredu podstavy. Osa x naseho souradneho systemu svira s osou x pravouhleho souradneho systemu uhel -30°. Osa y naseho souradneho systemu svira s osou x pravouhleho souradneho systemu uhel +30°. Pro lepsi ilustraci je na nasledujicim obrazku nakres peti typu celku z prvniho zadani z prikladu vstupu. Celky jdou na obrazku za sebou v tom poradi (zleva doprava a shora dolu), v jakem jsou uvedeny v prikladu vstupu.

Specifikace vystupu

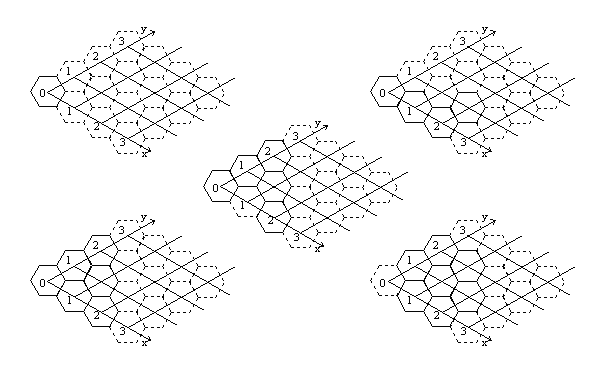
Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je uvedena veta ‘Je treba X celku.’, kde X je minimalni pocet celku, ktere jsou potreba pri optimalnim vyberu typu a optimalnim sestaveni nebo veta ‘Kapacita zakladny je pouze X lidi.’, pokud neni mozne z daneho poctu danych typu celku sestavit zakladnu pro dany pocet lidi.

Priklad vstupu

3
50 5
10 1 0 0
3 4 0 0 1 0 2 0 2 1
4 5 0 0 0 1 0 2 1 1 2 0
6 6 0 0 1 0 2 0 0 1 1 1 0 2
1 7 1 0 2 0 0 1 1 1 2 1 0 2 1 2
11 1
2 1 0 0
10 2
100 1 1 1
0 2 0 0 1 0

Priklad vystupu

Je treba 3 celku.
Kapacita zakladny je pouze 10 lidi.
Je treba 2 celku.

Problem E

Vyplneni prostoru

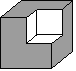
Hlavni sklad hyperkosmicke lodi Nostromo ma tvar trirozmerne krychle. Delka hrany krychle je mocninou 2. Ve skladu maji byt ulozeny baliky potravin a materialu ve tvaru krychle o delce hrany 2 bez jedne rohove elementarni krychlicky (viz obr. 1). Protoze objem baliku je pouze 7 elementarnich krychlicek, neda se sklad vyplnit beze zbytku. Organizatori vypravy tak museli resit problem, jak vyplnit sklad co nejlepe a to pokud mozno tak, aby zustala volny prostor jen o velikosti jedne elementarni krychlicky na definovanych souradnicich x, y, a z.

Vasim ukolem je napsat program, ktery dokaze rozhodnout, jestli pro danou velikost skladu a dane souradnice existuje rozmisteni baliku, ktere by splnovalo pozadavky konstrukteru a v kladnem pripade takove rozmisteni najit.

Obr. 1

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani tvori jeden radek, na kterem se nachazi ctyri cela cisla K, X, Y, Z oddelena mezerou, 1 <= k <= 8, 0 <= X <= 255, 0 <= Y <= 255, 0 <= Z <= 255. Velikost hrany krychle je 2K, volne misto o velikosti jedne elementarni krychlicky musi zustat na souradnicich X, Y, Z.

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek. V pripade, ze prostor nelze vyplnit podle pozadavku, musi tento radek obsahovat text ‘Prostor nelze optimalne vyplnit.’. Existuje-li reseni, musi radek obsahovat cele cislo M a dale pak M ctveric cisel X, Y, Z a O. Vsechna cisla na radku musi byt oddelena mezerou. M je pocet baliku, ktere se vejdou do skladu. X, Y, Z jsou souradnice kazdeho baliku a O je jeho otoceni. Otoceni O je definovano pozici chybejici osme elementarni krychlicky doplnujici balik na krychli 2x2x2 podle nasledujici tabulky:

O	X	Y	Z
0	0	0	0
1	1	0	0
2	0	1	0
3	1	1	0
4	0	0	1
5	1	0	1
6	0	1	1
7	1	1	1

Priklad vstupu

2
1 1 0 1
2 2 3 3

Priklad vystupu

1 0 0 0 5
9 1 1 1 7 0 2 2 1 2 0 2 2 0 0 2 3 2 2 0 4 0 2 0 5 2 0 0 6 0 0 0 7 2 2 2 6

Problem F

Prstencove generatory

Konstrukteri motoru hyperkosmicke lodi Nostromo museli vyresit problem se skladanim prstencovych generatoru. Tyto generatory slouzi k vedeni a tvarovani struktury proudu castic vytvarejicich hnaci pole. Generatory se skladaji z jednotlivych prstencu. Nektere prstence slouzi pouze jako distancni vlozky a proud castic nijak neovlivnuji, to jsou prstence ‘K’,’O’ a ‘Z’. Dalsi prstence urychluji nebo zpomaluji proudeni castic, ‘Q’ urychluje proud o 105 m/s, ‘B’ ho urychluje o 5.105 m/s, ‘M’ ho zpomaluje o 5.105 m/s a ‘T’ proud zpomaluje o 105 m/s. Castice proudi v koncentrickych vrstvach vzdalenych od sebe 0.1mm, tyto vrstvy se nemisi a urcite prstence pridavaji nebo ubiraji vrchni vrstvu. Prstenec ‘A’ pridava vrstvu elektronu, ‘E’ vrstvu neutronu a ‘I’ vrstvu pozitronu, prstenec ‘F’ odebira vrstvu elektronu, ‘W’ vrstvu neutronu a ‘U’ vrstvu pozitronu. Kazdy prstenec odebirajici nekterou vrstvu se poskodi neni-li na povrchu proudu castic ta vrstva kterou umi zpracovat. Zadny generator nesmi zacinat nebo koncit prstencem menicim rychlost proudeni a na konci z nej nesmi proudit jiz zadne castice. Jednotlive prstence nemohou nasledovat po sobe libovolne, ale musi splnovat omezeni shrnute v nasledujici tabulce:

Smi predchazet	Generator	Smi nasledovat
AEIQBMT	KOZ	QBMTFWU
FWUKOZ	QBMT	AEIKOZ
QBMTAEI	AEI	AEIKOZ
FWUKOZ	FWU	FWUQBMT

Kterykoliv prstenec z prvniho sloupce tabulky smi predchazet kterykoliv prstenec z prostredniho sloupce. Kterykoliv prstenec z tretiho sloupce tabulky smi nasledovat za kterykoliv prstencem z prostredniho sloupce. Priklad sestavy prstencu je na nasledujicim obrazku:

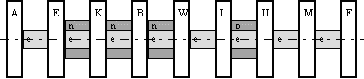
Vasim ukolem je napsat program, ktery overi navrh prstencoveho generatoru.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani je popsano jednim radkem. Na tomto radku se nachazi pismena velke anglicke abecedy. Pismena na sebe bezprostredne navazuji.

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je text ‘Tento prstencovy generator je funkcni.’, kdyz generator splnuje vyse uvedene podminky, jinak text ‘Tento prstencovy generator neni funkcni.’

Priklad vstupu

3
AKMKBAZMEKQKWTEMOWFFTEKW
AKFMEOW
EWEFW

Priklad vystupu

Tento prstencovy generator je nefunkcni.
Tento prstencovy generator je funkcni.
Tento prstencovy generator je nefunkcni.

Problem G

Optimalni trasa

Pri cestovani hyperprostorem patri zmena rychlosti nebo smeru hyperkosmicke lodi mezi velmi energticky narocne ukony. Z tohoto duvodu se tvurci lodi Nostromo rozhodli implementovat v palubnim pocitaci algoritmus, ktery pomuze naplanovat optimalni trasu. Za optimalni trasu povazujeme takovou trasu, kterou lze proletet s nejmensim energetickym vydajem. Soucasti tohoto algoritmu je i prohledani mnoziny bodu a nalezeni maximalniho poctu bodu, ktere lezi na jedne primce. Tato primka, vzhledem k vlastnostem pohonneho systemu, musi svirat s osou x nebo s osou y uhel 0°, +45° nebo -45°.

Vasim ukolem je napsat takovy program.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Prvni radek kazdeho zadani obsahuje prirozene cislo V - pocet zadanych bodu, V je z intervalu 1..1000000. Dale nasleduje V radku. Kazdy radek obsahuje prave dve cela cisla, oddelena mezerou, reprezentujici souradnice x a y jednotlivych bodu v rovine. Souradnice x a y jsou z intervalu 0..1000000.

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem se nachazi prave jedno cele nezaporne cislo udavajici maximalni pocet bodu, ktere lezi v jedne primce.

Priklad vstupu

Priklad vystupu

4
3

Problem H

Posloupnost planet

Hyperkosmicka lod Nostromo na sve ceste vesmirem navstivi velke mnozstvi planet v poradi jejich zajimavosti pro osidleni. Pri navrhu trasy lodi narazili organizatori vypravy na problem, ktery se pokusime zjednodusit a priblizit na problemu posloupnosti prirozenych cisel.

Mejme posloupnost prirozenych cisel A = {a₁, a₂, a₃, ..., a_N}, kde N je velke prirozene cislo. Rekneme, ze posloupnost B = {b₁, b₂, b₃, ..., b_M} je posloupnosti vybranou z posloupnosti A, prave tehdy, kdyz existuje takova posloupnost prirozenych cisel K = {k₁, k₂, k₃, ..., k_M}, ktera je rostouci a pokud pro kazde prirozene i, 1 <= i <= M, plati, ze b_i = a_{k_i}.

Vasim ukolem je napsat program, ktery najde pocet clenu nejdelsi neklesajici posloupnosti vybrane ze zadane posloupnosti A.

Specifikace vstupu

Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani obsahuje prvky urcite posloupnosti A pocinaje prvnim clenem a ukoncene cislem 0. Delka vstupni posloupnosti neni omezena. Hodnota kazdeho prvku je na samostatnem radku. Jednotliva zadani nasleduji bezprostredne za sebou.

Specifikace vystupu

Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je prave jedno prirozene cislo L - delka nejdelsi neklesajici vybrane posloupnosti. Delka nejdelsi neklesajici vybrane posloupnosti nepresahne 100000.

Priklad vstupu

Priklad vystupu

3
6