
 Zadani uloh
Zadani uloh
 Zadani uloh
Zadani uloh
Je dan obecny mnohouhelnik, jehoz vrcholy lezi v uzlech ctvercove souradnicove site. Diskretni obsah takoveho mnohouhelniku je pocet uzlu site lezicich uvnitr tohoto utvaru, pricemz uzlem lezicim uvnitr se mini uzel nelezici na zadne z hran mnohouhleniku takovy, ze pokud z nej vedeme libovolnou poloprimku nerovnobeznou s zadnou z hran, tak tato poloprimka protina hrany mnohouhelniku v lichem poctu bodu.
Vasim ukolem je napsat program, ktery vypocita diskretni obsah zadaneho mnohouhelniku.
Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Prvni radek kazdeho zadani obsahuje prirozene cislo V - pocet vrcholu mnohouhelniku, V je z intervalu 3..100000. Dale nasleduje V radku. Kazdy z techto V radku obsahuje prave dve cela cisla, oddelena mezerou, reprezentujici souradnice x a y jednotlivych vrcholu mnohouhelniku tak jak je prochazime jdouce po hranach proti smeru hodinovych rucicek. Souradnice x a y jsou z intervalu -100000..100000. Hrany spojuji vzdy vrcholy i a i+1 a navic vrcholy V a 1 (t.j. prvni a posledni vrchol). Zadne dva vrcholy nesplyvaji, zadne dve hrany nemaji spolecny vice nez jeden bod a zadna hrana neni degenerovana. Na obr. 1 je nakreslen mnohouhelnik, ktery odpovida prikladu vstupu a vystupu.
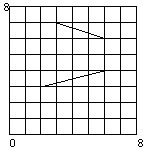
1 5 2 3 6 4 6 6 3 7 2 7
9
Hradlo AND je elektronicky logicky prvek se dvema vstupy a jednim vystupem realizujici logickou funkci 'a'. Na kazdem z jeho vstupu muze byt bud logicka uroven H nebo logicka uroven L. Potom hradlo na svem vystupu vytvori logickou uroven H prave tehdy, kdyz je na obou jeho vstupech uroven H, jinak na vystupu vytvori uroven L.
Sit hradel je jedno nebo nekolik hradel AND, ktera mohou byt navzajem propojena. Misto, kam je pripojen jeden nebo nekolik vstupu ci vystupu hradel, nazyvame uzel. Do jednoho uzlu smi byt pripojen nejvyse jeden vystup hradla a libovolny pocet vstupu hradel. Uzly rozeznavame dvou typu. Vstupni uzel - logicka uroven ve vstupnim uzlu je urcena obvody mimo sit. Vystup zadneho hradla nesmi byt pripojen do vstupniho uzlu. Vnitrni uzel - logicka uroven je urcena vystupem prave jednoho hradla. Vybrane vnitrni uzly, jejichz logicka uroven je pro nas zajimava, nazyvame vystupnimi uzly.
Kombinacni sit je takova sit hradel, ktera obsahuje pouze vstupni a vnitrni uzly a ktera neobsahuje cykly, t.j. stav na vystupu zadneho z hradel neovlivnuje stav na jeho vstupech. Potom stav ve vybranych vystupnich uzlech zavisi pro danou sit pouze na okamzitem stavu vstupnich uzlu. Popiseme logicke urovne ve vstupnich uzlech vektorem i = (i1, i2, i3, ..., iN) a logicke urovne ve vystupnich uzlech vektorem o = (o1, o2, o3, ..., oM), kde N je pocet vstupu, M pocet vystupu a prvky vektoru i a o jsou logicke urovne H nebo L. Pak rikame, ze kombinacni sit generuje transformacni funkci f(i) = o, pokud pro vsechny mozne hodnoty vektoru i, odpovidajicimu stavu vstupu, odpovida f(i) stavum vystupu.
Dve kombinacni site jsou ekvivalentni prave tehdy, kdyz maji stejny pocet vstupnich a vystupnich uzlu a generuji stejne transformacni funkce f1 a f2, tj. pro vsechny hodnoty vektoru i je f1(i) = f2(i).
Vasim ukolem je napsat program, ktery pro dane dve kombinacni site rozhodne,zda jsou ekvivalentni.
Vstup se sklada z K zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo K. Dale nasleduji jednotliva zadani. Prvni radka kazdeho zadani obsahuje dve prirozena cisla N a M odddelena mezerou, kde N je pocet vstupnich a M pocet vystupnich uzlu. M i N jsou nejvyse 100. Dalsi casti zadani jsou popisy dvou siti, z nichz kazda ma N vstupnich a M vystupnich uzlu. Prvni radek popisu kazde site obsahuje dve cisla U a H, kde U je celkovy pocet uzlu a H je pocet hradel site. U a H jsou prirozena cisla mensi nez 10000. Dale nasleduje H radku, kazdy popisujici jedno hradlo. Na kazde radce jsou tri prirozena cisla X, Y a Z, opet oddelena mezerami, reprezentujici hradlo se vstupy pripojenymi do uzlu X a Y a vystupem do uzlu Z, pricemz uzly 1..N jsou vstupni, uzly N+1..N+M vystupni a uzly N+M+1..U jsou ostatni vnitrni uzly. Na obr. 1 jsou nakresleny dve site, ktere odpovidaji prikladu vstupu a vystupu.
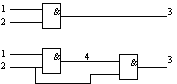
Obr. 1
Pro kazde zadani musi vystup obsahovat prave jeden radek obsahujici bud slovo 'Ano', pokud dane site jsou ekvivalentni, nebo slovo 'Ne', pokud ekvivalentni nejsou.
1 2 1 3 1 1 2 3 4 2 1 2 4 2 4 3
Ano
Mejme posloupnost prirozenych cisel A = {a1 , a2, a3, ..., aN} kde N je velke prirozene cislo. Rekneme, ze posloupnost B = {b1, b2, b3, ..., bM} je souvisla vybrana posloupnost z posloupnosti A, neboli podposloupnost posloupnosti A, prave tehdy, kdyz existuje takove cele k > 0, ze pro vsechna prirozena i, 1 <= i <= M, plati, ze bi = ak+i.
Vasim ukolem je napsat program, ktery najde pocet clenu nejdelsi neklesajici podposloupnosti zadane posloupnosti A.
Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani obsahuje prvky urcite posloupnosti A pocinaje prvnim clenem a ukoncene cislem 0. Delka vstupni posloupnosti neni omezena. Hodnota kazdeho prvku je na samostatnem radku. Jednotliva zadani nasleduji bezprostredne za sebou.
Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je prave jedno prirozene cislo L - delka nejdelsi neklesajici podposloupnosti. Delka nejdelsi neklesajici podposloupnosti nepresahne 100000.
1 1 8 2 3 0
2
Kazda zeme se dnes muze pochlubit svoji vlastni historii, specifickou kulturou a bohatymi tradicemi. Vetsina turistu si pak kupuje alespon kouse te tradice ve forme suvenyru nebo vyrobku, ktere jinde nesezene. Jen ve Svycarsku koupime nejkvalitnejsi hodinky, opravdovou pizzu ochutname v Italii, nejvetsi vyber originalnich kazet maji v Polsku. Pokud si z Ruska neprivezeme kvalitni vodku, zbydou nam penize na prave matrjosky.
Matrjosky jsou dute drevene panenky vyrobene v takovych velikostech, aby se vzdy mensi nechala uzavrit do vetsi. Kazda sada obsahuje nekolik panenek, ktere jsou bohate zdobeny.
Nas turista Pepa, pote co priletel z Ruska, pujcil suvenyr detem, ktere z jedne uplne sady slozily tri neuplne sady matrjosek. Pepa by rad slozil zpet puvodni jednu sadu, bohuzel vsak ma na svem stole zrovna vypisy disassemblovanych Windows95 a proto mu zbyva misto prave jen na tri matrjosky. Muze pouze nejvetsi panenku nektere ze tri neuplnych sad rozpulit, vyjmout zevnitr zbytek sady, umistit jej na misto, kde stala nerozpulena sada, a navleknout rozpulenou panenku na nekterou ze zbyvajicich sad na stole. Takovemu ukonu budeme rikat jeden tah. Cilem je slozit jednu uplnou sadu na co nejmene tahu.
Vasim ukolem je napsat program, ktery pro danou skladbu tri neuplnych sad dokaze urcit, na kolik tahu je mozne slozit z nich jednu uplnou sadu.
Matrjosky z puvodni uplne sady ocislujeme dle velikosti 1..M. Pokud jedna matrjoska ma cislo i a druha cislo j, i < j, pak matrjoska i je mensi a necha se uzavrit do matrjosky j. Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani se sklada ze ctyr radku. Prvni radek kazdeho zadani obsahuje prirozene cislo M - pocet matrjosek v uplne sade. Kazdy z dalsich trech radku popisuje jednu neuplnou sadu. Popis neuplne sady tvori rostouci posloupnost cisel matrjosek v neuplne sade. Cisla matrjosek jsou prirozena cisla navzajem oddelena mezerou. Posloupnost cisel matrjosek je ukoncena cislem 0.
Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je prave jedno cele nezaporne cislo T - minimalni pocet tahu, kterymi je mozne ze tri neuplnych sad slozit uplnou sadu matrjosek.
2 8 1 2 7 0 3 4 8 0 5 6 0 3 0 1 2 3 0 0
61 0
Necht pismeno je jeden ze znaku a-z, A-Z. Necht slovo je retezec pismen o delce alespon 1 a nejvyse 10. Text je posloupnost slov oddelenych navzajem alespon jednim z oddelovacu: mezera, nova radka, carka, tecka. Oznacme znaky v textu poradovymi cisly 1, 2, ..., N. Pak text vyjadrime jako posloupnost znaku t1t2t3...t4. Mejme dale slovo A = a1a2a3...am. Pro ucely vyhledavani slov v textu povazujme znaky male a velke abecedy za totozne. Rekneme, ze slovo A se vyskytuje v textu na pozici j prave tehdy, kdyz pro vsechna i = 1..m plati, ze ai = ti+j a je oddeleno od ostatnich slov oddelovacem, tj. (bud j = 0 nebo tj je oddelovac) a zaroven (bud i+j = N nebo ti+j+1 je oddelovac).
Vasim ukolem je napsat program, ktery zjisti, ktere z predem znamych slov se v textu vyskytuje nejcasteji.
Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani zacina radkem obsahujicim prirozene cislo S - pocet vyhledavanych slov, S < 1000. Na dalsich S radcich nasleduji vyhledavana slova, po dvou ruzna. Kazde slovo je na samostatnem radku. Pak nasleduje text skladajici se z radek o delce nejvyse 200 znaku. Text je ukoncen radkem, ktery obsahuje jako prvni znak na radku znak . (Tecka). Delka textu neni omezena, ale zadne slovo se v nem nevyskytne vice nez 100000 krat.
Pro kazde zadani musi vystup obsahovat prave jeden radek obsahujici slovo, ktere se v textu daneho zadani objevilo nejcasteji. Vyskytnou-li se dve slova v nekterem zadani stejne casto, vystup muze obsahovat libovolne z nich.
1 2 se sestrou Nesnese se se sestrou. .
se
Jiste jste jiz sledovali nejaky akcni film, ve kterem neporazitelny hlavni hrdina operoval na nepratelskem uzemi a pote co sam samotinky premohl armadu nepratel byl odvezen do bezpeci vrtulnikem. Nektere takove akce se odehravaji i v clenitem skalnatem terenu, kde vrtulnik muze pristat jen na nekterem miste a nas hrdina se k nemu musi sam dostat. V teto uloze se budeme zabyvat takovym pripadem.
Je dan popis uzemi obdelnikovou siti bodu, misto pristani vrtulniku a misto, ve kterem se nas hrdina nachazi. Popis jednoho bodu je jeho nadmorska vyska. Z kazdeho bodu lze primo prejit pouze do sousedniho bodu a to jen tehdy, jestlize je sousedni bod ve stejne vysce, o jednu jednotku vyse nebo o jednu ci dve jednotky nize. Sousednim bodem se rozumi bod vlevo, vpravo, vpredu ci vzadu. Jeden prechod trva jednu jednotku casu. Vasim ukolem je napsat program, ktery pro takoveto zadani urci nejmensi cas, ktery hrdina potrebuje na to, aby se dostal k vrtulniku.
Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Zadani jednoho prikladu ma tento format:
X Y bX bY eX eY Y radek s X cisly
X, Y : rozmer mapy; prirozena cisla z intervalu 1..1000 oddelena mezerou bX, bY : souradnice mista, kde se naleza nas hrdina eX eY : misto, kde pristane vrtulnik bX, eX jsou cela cisla z intervalu 0..X-1 oddelena mezerou bY,eY jsou cela cisla z intervalu 0..Y-1 oddelena mezerouY radek s X cisly je vlastni popis uzemi za pomoci nadmorskych vysek jednotlivych bodu. Nadmorska vyska bodu je cele cislo z intervalu 0..1 000 000 000.
Pro kazde zadani musi vystup obsahovat jeden radek s textem 'Hrdina se k vrtulniku dostane za x casovych jednotek.', kde x je minimalni cas, ktery nas hrdina potrebuje, aby se dostal z bodu [bX,bY] do bodu [eX,eY]; pripadne text 'Hrdina se k vrtulniku vubec nedostane.', pokud se hrdina z bodu [bX,bY] do bodu [eX,eY] vubec nemuze dostat.
4 4 5 0 2 0 0 14 15 17 16 5 5 5 18 10 5 5 17 11 12 13 16 12 12 14 15 4 5 0 2 1 1 14 15 17 16 5 5 5 18 10 5 5 17 11 12 13 16 12 12 14 15 2 1 0 0 1 0 67 45 6 1 5 0 0 0 1 2 4 6 5 5
Hrdina se k vrtulniku dostane za 12 casovych jednotek. Hrdina se k vrtulniku vubec nedostane. Hrdina se k vrtulniku vubec nedostane. Hrdina se k vrtulniku dostane za 5 casovych jednotek.
Mejme posloupnost prirozenych cisel A = {a1, a2, a3, ..., aN}, kde N je velke prirozene cislo. Rekneme, ze posloupnost B = {b1, b2, b3, ..., bM} je posloupnosti vybranou z posloupnosti A, prave tehdy, kdyz existuje takova posloupnost prirozenych cisel K = {k1, k2, k3, ..., kM}, ktera je rostouci a pokud pro kazde prirozene i, 1 <=; i <= M, plati, ze bi = aki.
Vasim ukolem je napsat program, ktery najde pocet clenu nejdelsi neklesajici posloupnosti vybrane ze zadane posloupnosti A.
Vstup se sklada z N zadani. Prvni radek vstupniho souboru obsahuje prirozene cislo N. Dale nasleduji jednotliva zadani. Kazde zadani obsahuje prvky urcite posloupnosti A pocinaje prvnim clenem a ukoncene cislem 0. Delka vstupni posloupnosti neni omezena. Hodnota kazdeho prvku je na samostatnem radku. Jednotliva zadani nasleduji bezprostredne za sebou.
Pro kazde zadani musi vystup obsahovat prave jeden radek, na kterem je prave jedno prirozene cislo L - delka nejdelsi neklesajici vybrane posloupnosti. Delka nejdelsi neklesajici vybrane posloupnosti nepresahne 100000.
1 1 8 2 3 0
3