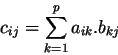
Problems Statement of CTU Open 1999 Contest

Department of Computer Science, CTU FEE & Czech ACM Chapter

CTU Open Contest 1999

This is an unofficial translation only. We have only several hours to do it so the language is not very good. But you should be able to understand all the problems.

Dear Contestants:

As every year, we have prepared a set of real life problems. This time it is the composing of excelent Collection of favourite scientific, desk and card games (Kolekce oblibenych kolektivnich odbornych, deskovych a karetnich her), with the acronyme KOKODáKH. It should contain many traditional and even only little known games. We expect a big comercial success after releasing it. We would be glad if you could help us with that interesting topic. We decided that one half of all the profit should be divided among the contestants with the respect to number of solved problems. So you have one more motivation to do your best and start to solve the problems.

The GUI was given to another firm, so we are interested in the efficient algorithms only. All the programs you have to create should read the data from the standard input and write the result to the standard output. You must follow the given format exactly in order to allow integration with the GUI. When there are more values on the same line, they are divided using exactly one space, if not specified otherwise. Neither input nor output may contain unneeded spaces and lines.

Because some situations require batch processing of more input cases, your programs must be able to solve more instances of the problem at once. Usually there is the total number of problems specified on the first line. Then the particular cases follow. The exact format is specified for each of the problems. If the input contains any integer numbers, they are only so big to fit into standard integer type (if not specified otherwise). Also the result should fit into it (if not specified otherwise).

Well, all we need to do now is to wish you Good Luck.

Your Organization Team

Jack

(file name: jack.c, jack.p, jack.C)

We need to have at least one computer game in our collection, of course. The typical one could be described as "chase in the town". The smiling face called Jack in our case is walking through the town divided into small fields. Some of the fields are covered with the wall and it is not possible to go through them. Jack collects the points and tries to avoid contact with the monsters who chase him. Once the Jack eats the special point (or asterisk), the situation turns upside-down and Jack can eat monsters. And so on, still again and again. I am sure everyone of you have ever seen such game.

The town is randomly generated in our case. Jack always starts in the top left corner and the "bonus asterisk" is in the bottom right corner. At the most difficult level, the bonus is set to disappear after exactly as much steps that are sufficient to get from one corner to another, providing Jack only makes steps to the left and to the bottom. Should he made one single step into the wrong direction and he never could be there in time. But it is still important to prevent being catched by monsters. So the player has to choose the best possible way to the bottom right corner. You are to determine how many different ways exist in the town.

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. Each assignment begins with the line containing two possitive numbers R and S (1 <= R,S <= 1000). The numbers determine the number of town rows and columns. Then there are R lines each containing exactly S characters. Each character may be either hash (#) or period (.). Hash mark means the wall and the period is free space. The top left and bottom right corners are always free.

Output Specification

Print exactly one line for each of the input cases. The line must contain the statement "Existuje X ruznych cest.", (There are X different paths). Replace X with the number of all existing different paths between the top left and the bottom right corner. Each path must consist of R+S-2 steps, each leading to the left or to the right. No path can cross any field with the wall.

Sample Input

2
3 3
...
.#.
...
1 6
...#..

Output for the Sample Input

Existuje 2 ruznych cest.
Existuje 0 ruznych cest.

Kaleidoskop (Caleidoscope)

(file name: kaleidoskop.c, kaleidoskop.p, kaleidoskop.C)

We suppose even the very little children will play with KOKODáKH. So beside all the games and riddles, we need to have at least one toy in it. It is very favourite one and no special knowledge or ability is required to play with it. Yes, it is the Caleidoscope. I guess all of you know the magic thing. You can watch into it for long hours and still find new and new images that never repeat. But there is a problem with the little children. They break everything they have, all the things are falling from their hands down to the ground. The mechanics of caleidoscope is very fine and so it is very sensitive to proper handling. So our variant of this toy is not mechanical but fully electronic one. The main advantage is that it is water-resistant, fire-resistant, cold-resistant, it cannot break and does not catch fire. Besides, it contains a special teeth detector that prevents the children to bite it. Every tooth contact is detected and reacts with the electric shock (@@@) immediately.

The main problem with our electric caleidoscope is the picture generating. To reach the quality of the mechanical caleidoscope, the picture must consist of many similar pieces that are resized, mirrored and rotated. As many of you probably know, we use matrices in computer graphics to manipulate pictures. The so called transformation matrix specifies the action that should be done with the picture. The picture manipulation is then done by matrix multiplication. We can also preform many transformations sequentially, by multiplying with more matrices. The picture manipulation is very difficult in the caleidoscope, so the matrices can be very large. Your task is to write a computer program that would be able to multiple the given matrix with the sequence of other matrices.

When we multiple the matrix A (dimensions m x p) with the matrix B (dimensions p x n) we get the matrix C with the dimensions m x n. Every item with the indices i and j in the resulting matrix is the scalar product of the i-th row of maxtrix A and j-th column of matrix B:

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. Each assignment begins with the line containing the single number X (1 <= X <= 10000) stating for the number of matrices. Then there are exactly X matrix descriptions. Each description begins with the line containing two integers M and N (1 <= M,N <= 100). M is the number of rows, N the number of columns. After these numbers there are exactly M lines each of them containing N integers seperated by space. These numbers are the matrix items. You can assume that the matrices really can be multipled. That means M of every matrix (except the first one) is the same as N of the previous one. The numbers are only as high that the items of resulting matrix should fit into integer. Also the items of every "partial result matrix" should fit there, when you will multiple them sequentially.

Output Specification

The program should print out the resulting matrix for each assignment, with the dimensions m x n. The output should consist of m lines, each containing n numbers separated by exactly one space. Print one empty line after each assignment including the last one. Empty line contains one the special character newline.

Sample Input

Output for the Sample Input

Logik (Logic)

(file name: logik.c, logik.p, logik.C)

There is also the logical game "Of Liars and Honest Men" in our KOKODáKH collection. Almost any number of players can participate in the same game and no special items are needed. The rules are simple: every player tosses a coin to decide if he is Liar or Honest. All the other players know what he is. After all of the roles are determined, the play begins. Honest men must tell the truth under any circumstances, liars must always lie. Whoever should violate this simple rule, he (or she) loses that game. You would not believe how interesting this game can be! Good players can assemble (@@) even very complicated statement and it is very difficult to determine its meaning. Excellent players can play this game for several days without making a mistake. Their children and wives search them all over the town without any success.

The players consider for the best situation, when some other person enters the room and listens to them. Of course the players won't stop! They want to impress the new person and the statements become even more complicated. The witness (@@@) has the only possibility. He must to listen very carefully and determine who is who. The best for him is to prove someone's mistake because it should ended the game. Unfortunately, this is not easy. You are to write a computer program that will be able to listen the conversation and tries to determine who is liar.

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input.

Each assignment begins with one empty line that separates it from the previous text. Then there is the single number P (1 <= P <= 10) stating the number of players. Then exactly P lines follow, each containg name of one player. The name consists of letters only, the first one is capital, all the others are lowercase. In the remaining input, the names are always given in the exactly same form as the first time. Every name has at least one and at most ten characters. No name can be "Lharu" or "Poctivcu".

Then there is a single number M (0 <= M <= 500) on the separate line. This is the number of formulas to follow. Then there are exactly M lines, each of them has the exact format: name of the player, colon, one space, the formula and period. No line can be longer than 1000 characters. The formula has one of the forms (X,Y,Z are non-negative integers; H,F are player names; V,W are formulas). Note that the formula of type 4 ends with a period, any other formula does not.

1.: X + Y = Z
2.: H je poctivec (H is Honest)
3.: H je lhar (H is Liar)
4.: H rika "V". (H says V)
5.: H rika "V" a je to opravdu tak (H says V and it's really true)
6.: H rika "V", ale neni to pravda (H says V but is lying)
7.: Poctivcu je mene nez X (There are less than X Honests)
8.: Poctivcu je vice nez X (There are more than X Honests)
9.: Poctivcu je alespon X (There are ate least X Honests)
10.: Lharu je mene nez X (There are less than X Liars)
11.: Lharu je vice nez X (There are more than X Liars)
12.: Lharu je alespon X (There are ate least X Liars)
13.: (V) a zaroven (W) ((V) and (W))
14.: (V) nebo (W) ((V) or (W))

The formula of type 4 is true if and only if the player H could say the formula V without breaking the rules (that means if V is not true and H is liar, or if V is true and H is honest). Formulas 5 a 6 consist of two independent formulas ("H says V" and "V is [not] true"). If the author of the formula is liar, both of these parts must be false. If he is honest, both parts must hold. The formula consisting of one true part and one false part is called non-satisfiable (@@@) and noone can say it without breaking the rules. The formulas 7 through 12 mean the total number of liars (or honests) so the author of the formula also counts. Formula 13 is true if the both parts are true, and false, if any of them is not true. The formula 14 is true if any of its parts is true. If any of the parts of the formula of type 13 or 14 is non-satisfiable, it is counted as if it was false. Even two non-satisfiable formulas connected with the and or or give false result (not non-satisfiable result). That means that liar can say such formula.

Output Specification

Print the line "Hra cislo X:" (The game number X) for each assignment. Replace X with the number of the assignment, starting with one.

As the first step, assume that no player violated the rules, that means liars say false formulas and honests say the truth. If there exists such arrangement of players that all the formulas could be said, the set of formulas is called satisfiable. If the input contains a satisfiable set, the program has to print all the roles that can be certainly determined. Every such role must be reported on the separate line of the form: "H je lhar." (H is liar) or "H je poctivec." (H is honest). If there are more roles to be reported, they should be printed in the same order as the player names on the beginning of input file. If it is not possible to determine any player's role, the program should print the line "Neda se nic zjistit." (Nothing could be deducted).

If the set of formulas is not satisfiable, it is obvious that someone has violated the rules and has lost the game. So we should try to determine who was that. Assume that only one player did the mistake. If the player F has violated the rules, we must not take all of his formulas into consideration. It means only the "main" formulas said by that player. All the "included" formulas of type "F says V" are still valid because their semantics are "F could say V following all the rules".

If there is exactly one player after removing whose "main" formulas we get the satisfiable set, the program should print the line "F prohral." (F has lost). If there are more such players, the output should be: "Prohral nektery z techto hracu: F1, F2, F3." (Some of the following players has lost: F1, F2, F3).

If there is no such player whose formulas we could remove to get the satisfiable set, the program is to print the line: "Pravidla porusilo vice hracu." (The rules were violated by more players).

Print one empty line after each assignment including the last one. Empty line contains one the special character newline.

Sample Input

2

3
Petr
Josef
Marie
1
Petr: Petr je lhar.

3
Petr
Josef
Marie
1
Josef: Marie rika "Marie je lhar" a je to opravdu tak.

Output for the Sample Input

Hra cislo 1:
Petr prohral.

Hra cislo 2:
Josef je lhar.
Marie je poctivec.

Mocneni (Raising Modulo Numbers)

(file name: mocneni.c, mocneni.p, mocneni.C)

People are different. Some secretly read magazines full of interesting girls' pictures, others create an A-bomb in their cellar, others like using Windows, and some like difficult mathematical games. Latest marketing research shows, that this market segment was so far underestimated and that there is lack of such games. This kind of game was thus included into the KOKODáKH. The rules follow:

Each player chooses two numbers A_i and B_i and writes them on a slip of paper. Others cannot see the numbers. In a given moment all players show their numbers to the others. The goal is to determine the sum of all expressions A_i^B_i from all players including oneself and determine the remainder after division by a given number M. The winner is the one who first determines the correct result. According to the players' experience it is possible to increase the difficulty by choosing higher numbers.

You should write a program that calculates the result and is able to find out who won the game.

Input specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. Then the assignements follow. Each assignement begins with line containing an integer M (1 <= M <= 45000). The sum will be divided by this number. Next line contains number of players H (1 <= H <= 45000). Next exactly H lines follow. On each line, there are exactly two numbers A_i and B_i separated by space. Both numbers cannot be equal zero at the same time.

Output specification

For each assingnement there is the only one line of output. On this line, there is a number, the result of expression

(A₁^B₁ + A₂^B₂ + ... + A_H^B_H) mod M.

Sample Input

3
16
4
2 3
3 4
4 5
5 6
36123
1
2374859 3029382
17
1
3 18132

Output for the Sample Input

2
13195
13

Nejvyssi zisky (The Highest Profits)

(file name: nejvyssi.c, nejvyssi.p, nejvyssi.C)

This program will not be part of the KOKODáKH collection, but it may be more important than the games themselves. It will serve to the marketing staff to find suitable procedures for promoting and selling the collection. So try to do your best.

Extensive marketing case study tried to prove that the total income from selling a product is polynomial function of number of satisfied customers. Experiments showed that the real results are not exactly the same which you can obtain using the function. However, this method is widely used. The reason is probably nonexistence of better solution. Let's denote the number of satisfied customers y, than we can express profits (denoted x) as

x = P(y) = a₀ + a₁.y + a₂.y² + ... + a_m.y^m

The number of satisfied customers depends on the price of a product. Again, there is hypothese that this dependence is polynomial. If we denote the price z, we can write

y = Q(x) = b₀ + b₁.z + b₂.z² + ... + b_n.zⁿ

Coeficients a_i and b_i strongly depend on the season of the year, the moon phase, the purchasing power of customers, inflation rate and hunderds of other parameters. Besides on the kind of product and its quality, of course. In the past there was lot of effort put into the reserarch of these parameters. For various combinations of input parameters, the coeficients are stated in Pyshwejc's marketing tables. It is not thus difficult to find out their values. But the degree of polynoms is usualy very high. It is very difficult to substitute one polynom into the other and to compute the dependency of the profit on the price. This dependency is usually crucial for us to set the right price.

Your goal is to write the program which can substitute the polynom Q into the polynom P and determine the restulting polynom R indicating dependency of the profit on the price:

x = R(z) = c₀ + c₁.z + c₂.z² + ... + c_p.z^p

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. Each assingement constist of three lines. On the first line there are two integers m and n (0 <= n,m <= 100) separated by space. These numbers give the degree of polynoms Q and P. On the second line there are m+1 integers a₀ ... a_m. These numbers are coeficients of polynom P. On the third line there are n+1 integers b₀ ... b_n. Always a_m <> 0 and b_n <> 0. Coeficients a_i and b_i are separated by space and they are chosen in order to each resulting coeficient could fit into the standard type integer.

Output Specification

The program prints exactly one line for each assignement. On this line, there will be p+1 numbers. These numbers are coeficients c₀ ... c_p of resulting polynom. The coeficients are separated by space and the line does not consist any redundant spaces. The coeficient in the highest degree should not be zero.

Sample Input

Output for the Sample Input

7
60 -36
-3 18 -63 123 -156 138 -86 36 -9 1

Osmismerka (Word Puzzle)

(file name: osmismerka.c, osmismerka.p, osmismerka.C)

What a game collection it would be without famous and well known word puzzle. Also KOKODáKH contains this game. Typical word puzzle is a rectangular array filled with letters, and the list of words. The goal is to find the words form the list in the array and to score out all their letters. After scoring out the letter can still be part of any other word (words can cross and overlap). When all words from list are found and scored out there are several remaining letters. These letters, read in rows, create the secret word. The words can be found in all eight directions, including diagonal directions.

It is clear that KOKODáKH has to bring some innovation into this game. The new rule says that the word can "jump over" the array boundary and continue on the opposite side. Upper row is thus next to the bottom row and the left collum is next to the right one. If we number the rows with numbers 0 till R-1 and collums with numbers 0 till S-1, we can describe each field in the array by the coordinates. For example (0,0) is the upper left corner. Word beginning on the position (x,y) can be created by succesion of characters with coordinates (x,y), ((x+i+R) mod R, (y+j+S) mod S), ((x+2i+R) mod R, (y+2j+S) mod S) and so on. The i and j can be substitued by numbers -1, 0 and +1, but they cannot be both zero at the same time.

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. The assignements follow. Each assignement consists of array filled with letters, and the list of words which should be found in the array. The description of the array begins with the line containing two integers R and S separated by space 1 <= R,S <= 200. R is the number of rows in the array, S is the number of collumns. The R lines follows, each line constist of exactly S lowercase letters (a trough z). The next line is the integer K (0 <= K <= 1000) determining the number of words to be found out in the puzzle. The K lines follow. On each line, there is one word. The maximum length of the word is 20 characters. The word may not appear in the array and it can appear there several times. In this case all appearences are scored out. Words in the list can repeat.

Output Specification

The program prints one line for each assignement. On this line there will be all letters from word puzzle which remained in the array after scoring out all the words that appeared on the list. The letters are not separated and they are lined up in order in which they appeared in the array in row major order. At the end of the string, there is the newline character. If there are no remaining letters after scoring out all words, the program prints out empty line.

Sample Input

1
3 7
kroksun
pranyra
cmakrom
7
syr
kra
kroksunkrok
pranyr
rak
mak
makro

Output for the Sample Input

acm

Patnactka (Lloyd Fifteen Puzzle)

(file name: patnactka.c, patnactka.p, patnactka.C)

Nearly everybody knows the popular game called Lloyd fifteen puzzle. The puzzle consists of fifteen numbered tiles placed in the square box. The dimensions of the box are 4 x 4, one place is free. The goal is to sort the tiles by moving the neighbouring ones to the free position. In the end the tiles should be orderd by their numbers. The tile with number 1 will be in the left upper corner and next tiles are ordered in row major order. The last position (the right bottom corner) will be free.

Also KOKODáKH contains the modification of this game. The game is destinated for the advanced players so the fifteen tiles would be too little. Our game can have arbitrary dimension of the array. Your goal is to write the program which will simulate the working of this game. For a given starting situation it has to replay the succession of valid moves and to display the final state of the puzzle. The valid move is moving the tile to the neighbouring free position up, down, right or left. Any other move is not valid.

Input Specification

At the first line of the description of the game initialposition, there are two integers R and S (2 <= R,S <= 1000) separated by space. R is a number of rows, S is number of columns. The R lines of input describing the rows of the puzzle follow. On each line there is S integers separated by at least one and at most ten spaces. At the begining of the line can be up to ten spaces which should be ignored. There are no spaces at the end of the line. Each number is the number of the tile in the given line. First number in the first line corresponds to the upper left corner of the puzzle. All numbers are between 0 to R.S-1 (inclusive) and each number appeares only once. Zero appear also only once and gives the position of the empty field.

The list of moves follows. The list can be empty. Each move is on the separate line and consists of one number T (0 < T <= R.S-1), which is the number of the tile which should be moved. At the end of the list there is the line containing number 0. Zero indicates the end of input and is not the part of the list of moves.

Output Specification

For each assignement the program prints out one line "Skladacka cislo C:" (Puzzle number C) where C is substitued by the number of the assignement. The numbering of assingement is ascending and begining with 1.

For each move in the list the program finds out if the move is valid. The move is valid if there is an empty field neighbouring. For each valid move the program prints out the following sentence at the separate line: "Kamen T presunut KAM." The tail number T moved KAM), where T is the number of the tile and KAM is one of the strings "doprava", "doleva", "nahoru" nebo "dolu" (right, left, up, down). If the move is not valid the sentence "Neplatny tah kamenem T." (Invalid move with tile T) is printed out.

When the list of moves ends, the program prints out the final state of the puzzle in the similar format that was used in the input. The output has to consist of R lines, each containing S numbers. The only difference from the input format is separating number by exactly one space. After each assignement (including the last one) the program prints out the empty line. Empty line consists only of the newline character.

Sample Input

2
4 4
 1  2  3  4
 5  6  7  8 
 9 10 11 12
13 14 15  0
15
11
7
0
4 4
 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14  0 15
1
0

Output for the Sample Input

Skladacka cislo 1:
Kamen 15 presunut doprava.
Kamen 11 presunut dolu.
Kamen 7 presunut dolu.
1 2 3 4
5 6 0 8
9 10 7 12
13 14 11 15

Skladacka cislo 2:
Neplatny tah kamenem 1.
1 2 3 4
5 6 7 8
9 10 11 12
13 14 0 15

Quorf

(file name: quorf.c, quorf.p, quorf.C)

To keep the word "card" in its name, KOKODáKH also contains one less known card game called Quorf. You need three idetical card packets. The kind of card is not important you can use for example only numbered cards. Each card can appeare only once in each packet. During the game, two players prepare the task for the third player and he tries to solve it. The game, under some conditions, can be played also as a solitaire, i.e. the game for one player. KOKODáKH contains this modification of the game. The program you are to write will be at the place of the two players preparing the task.

The principle of the game is very easy. Each of two preparing players chooses for one packet arbitrary cards and shuffle them in the order which cannot be changed later. The "main" player can then look at both packets and orders his third pakcet in arbitrary order. Of course he tries to choose the order in the way which enables him to win in the following game.

During the game both players (in our case represented by the program) turn the upper card from their packets and put it at the table. Main player then turns the cards from his packet and puts them at the table. If he turns a card that already appears on the table by one of the other players, that player's card is put out of game. If both players has the same card and the main player turns it, both their cards are put out of game. Games continues until the main player has cards in his packet. Then, if any of two players has any card, the main player losts. If neither of the two players has any card, third player won.

The program plays the role of the two players. Generating the contents of both packets is not difficult problem. More difficult is to find out whether the third player can win. Your task is to write program that will be able to determine this.

Input Specification

The input consists of Z assignments. The number of them is given by the single positive integer Z appearing on the first line of input. The assignements follow. Each assignement begins with line containing two numbers N and M (1 <= M,N <= 100000) separated by space. Two lines follow. At the first line, there are N numbers a_i separated by space. At the second line there are M numbers b_i. These numbers give the order of the cards in the packets of both preparing players. No number can appear twice in the same succession. Thus, for each i,j if a_i = a_j or b_i = b_j then i = j.

Output Specification

The goal of the program is to determine for each assignment whether there is a succession c₁, c₂, ..., c_x such that no number appeares twice in this succession and the order of the cards leads to the victory. If such succession exists, the program prints out the only line containing the sentence "Hrac ma sanci vyhrat." (The player can win). If there is no such succession, the input is the sentece "Spatne usporadani." (Wrong order).

Sample Input

Output for the Sample Input

Spatne usporadani.
Hrac ma sanci vyhrat.