Czech ACM Student Chapter CTU in Prague, Dept. of Computer Science and Engineering Charles University in Prague, MFF VİB TU Ostrava, FEI, Dept. of Computer Science SUT Bratislava, FEI, Dept. of Computer Science and Engineering CTU Open 2003 Dear contestants: We have prepared a set of real-life problems for you. This time, we are working for a goods transportation company called Advanced Cargo Movement, Ltd. (ACM). When delivering cargo, the company drivers and other employees have to cope with many problems. Some of them can be solved with the help of computers. You are to write several programs to help ACM with their work. All of the programs will run in UNIX environment. Every program should read data from the standard input and send results to the standard output. The data format is given and must be exactly followed. There will be no extra spaces in the input and there should be no extra spaces and newlines in the output, if not stated otherwise. The end-of-line character is not considered a part of the line. We wish you a lot of fun and good luck with solving these problems. Your organizing team intro.ps.gz All problems have been prepared by students from CTU in Prague, in cooperation with students from Charles University in Prague. All problems are original, except the problem traffic, which has been taken from SouthEast USA Regional Contest 1999.         C Pascal in out PostScript Bridge Hands bridge.c bridge.p bridge.in.gz bridge.out.gz bridge.ps.gz Charlie's Change change.c change.p change.in.gz change.out.gz change.ps.gz Building a New Depot depot.c depot.p depot.in.gz depot.out.gz depot.ps.gz Truck History history.c history.p history.in.gz history.out.gz history.ps.gz Base Numbers numbers.c numbers.p numbers.in.gz numbers.out.gz numbers.ps.gz Paper Cutting paper.c paper.p paper.in.gz paper.out.gz paper.ps.gz Hexagonal Routes routing.c routing.p routing.in.gz routing.out.gz routing.ps.gz Storehouse store.c store.p store.in.gz store.out.gz store.ps.gz Traffic Jam traffic.c traffic.p traffic.in.gz traffic.out.gz traffic.ps.gz all.tar Bridge Hands bridge.c, bridge.p bridge.in.gz, bridge.out.gz bridge.ps.gz Drivers of Advanced Cargo Movement, Ltd. usually have to wait quite a long time when waiting at border crossings for duty clearance. They are used to play various (card) games to have some fun. One of the games is Bridge. Playing Bridge involves dealing a standard deck of 52 cards to 4 players, so that each player receives 13 cards. Good players can then play with the hand as it is dealt, but most ordinary players will need to sort it, firstly by suit and then by rank within suit. There is no fixed ranking of the suits for this purpose, but it is useful to alternate the colors, so we will presume the following ordering: (club) < (diamond) < (spade) < (heart). (Note that because most character sets do not recognize these symbols, from now on we will use the more conventional C, D, S, and H). Within a suit, Ace is high, so the ordering is 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < T < J < Q < K < A . The players are usually called North, South, East, and West as they sit at the points of the compass. One player is designated the dealer and she deals one card to each player starting with the player on her left and proceeding clockwise until she deals the last card to herself. Write a program that will read in a representation of a deck of cards, deal them, sort them, and then display four sorted hands in the format shown below. Input Specification The input consists of a series of deals. Each deal begins with a line containing a single letter representing the dealer ("N", "E", "S", "W") followed by two lines representing the deck, card by card, as shown below. The first card given in the input is the first one to be dealt. The file is be terminated by a line consisting of a single hash character ("#"). Output Specification Output should consist of a series of sets of 24 lines, one set for each deal, separated by blank lines. Each set will consist of four groups of six lines displaying the sorted hands, in the order of their suit and rank. Use the format shown below. South player always goes first. Sample Input N CQDTC4D8S7HTDAH7D2S3D6C6S6D9S4SAD7H2CKH5D3CTS8C9H3C3 DQS9SQDJH8HAS2SKD4H4S5C7SJC8DKC5C2CAHQCJSTH6HKH9D5HJ # Sample Output South player: +---+---+---+---+---+---+---+---+---+---+---+---+---+ |3 3|5 5|7 7|T T|J J|9 9|T T|J J|3 3|K K|2 2|9 9|T T| | C | C | C | C | C | D | D | D | S | S | H | H | H | |3 3|5 5|7 7|T T|J J|9 9|T T|J J|3 3|K K|2 2|9 9|T T| +---+---+---+---+---+---+---+---+---+---+---+---+---+ West player: +---+---+---+---+---+---+---+---+---+---+---+---+---+ |2 2|4 4|K K|4 4|5 5|6 6|Q Q|A A|4 4|8 8|T T|J J|8 8| | C | C | C | D | D | D | D | D | S | S | S | S | H | |2 2|4 4|K K|4 4|5 5|6 6|Q Q|A A|4 4|8 8|T T|J J|8 8| +---+---+---+---+---+---+---+---+---+---+---+---+---+ North player: +---+---+---+---+---+---+---+---+---+---+---+---+---+ |6 6|8 8|9 9|A A|8 8|9 9|A A|4 4|5 5|6 6|7 7|J J|A A| | C | C | C | C | D | S | S | H | H | H | H | H | H | |6 6|8 8|9 9|A A|8 8|9 9|A A|4 4|5 5|6 6|7 7|J J|A A| +---+---+---+---+---+---+---+---+---+---+---+---+---+ East player: +---+---+---+---+---+---+---+---+---+---+---+---+---+ |Q Q|2 2|3 3|7 7|K K|2 2|5 5|6 6|7 7|Q Q|3 3|Q Q|K K| | C | D | D | D | D | S | S | S | S | S | H | H | H | |Q Q|2 2|3 3|7 7|K K|2 2|5 5|6 6|7 7|Q Q|3 3|Q Q|K K| +---+---+---+---+---+---+---+---+---+---+---+---+---+ Charlie's Change change.c, change.p change.in.gz, change.out.gz change.ps.gz Charlie is a driver of Advanced Cargo Movement, Ltd. Charlie drives a lot and so he often buys coffee at coffee vending machines at motorests. Charlie hates change. That is basically the setup of your next task. Your program will be given numbers and types of coins Charlie has and the coffee price. The coffee vending machines accept coins of values 1, 5, 10, and 25 cents. The program should output which coins Charlie has to use paying the coffee so that he uses as many coins as possible. Because Charlie really does not want any change back he wants to pay the price exactly. Input Specification Each line of the input contains five integer numbers separated by a single space describing one situation to solve. The first integer on the line P, 1 P 10 000, is the coffee price in cents. Next four integers, C1, C2, C3, C4, 0 Ci 10 000, are the numbers of cents, nickels (5 cents), dimes (10 cents), and quarters (25 cents) in Charlie's valet. The last line of the input contains five zeros and no output should be generated for it. Output Specification For each situation, your program should output one line containing the string "Throw in T1 cents, T2 nickels, T3 dimes, and T4 quarters.", where T1, T2, T3, T4 are the numbers of coins of appropriate values Charlie should use to pay the coffee while using as many coins as possible. In the case Charlie does not possess enough change to pay the price of the coffee exactly, your program should output "Charlie cannot buy coffee.". Sample Input 12 5 3 1 2 16 0 0 0 1 0 0 0 0 0 Sample Output Throw in 2 cents, 2 nickels, 0 dimes, and 0 quarters. Charlie cannot buy coffee. Building a New Depot depot.c, depot.p depot.in.gz, depot.out.gz depot.ps.gz Advanced Cargo Movement, Ltd. is successfully expanding. In order to meet new demands on truck maintenance, the management of the company decided to build a new truck depot. A suitable lot for building a depot was purchased and a construction company ``Masonry and Fences for Future, Ltd.'' was hired to build a depot. The area of the depot will be enclosed by a fence. The fence is supposed to enclose a connected area of a lot and each part of the fence follows North-South or East-West direction. At each place where the fence changes its direction, there is a single post. The posts are only at points where the fence changes the direction, i.e., there are no unnecessary posts. When MFF workers have built all of the posts, they lost the plan of a depot being built. At this moment, they asked you for a help. Given the coordinates of all the posts, your task is to compute the length of the fence. Input Specification The input consists of several blocks. The first line of each block contains a single number P, 1 P 100 000. P is the number of posts which have been built. Each of the following P lines contains two integers X and Y, 0 X, Y 10 000, which represent coordinates of the posts in MFF internal units (which no one else is able to understand). No two posts have the same coordinates. Each block is followed by a single empty line and the input is terminated by a line containing a single number 0. Output Specification Output contains a single line for each block. The line should contain the text "The length of the fence will be L units.", where L is replaced by an actual length of the fence. You can assume that the fence can always be built. Sample Input 6 1 1 1 3 3 3 2 1 3 2 2 2 0 Sample Output The length of the fence will be 8 units. Truck History history.c, history.p history.in.gz, history.out.gz history.ps.gz Advanced Cargo Movement, Ltd. uses trucks of different types. Some trucks are used for vegetable delivery, other for furniture, or for bricks. The company has its own code describing each type of a truck. The code is simply a string of exactly seven lowercase letters (each letter on each position has a very special meaning but that is unimportant for this task). At the beginning of company's history, just a single truck type was used but later other types were derived from it, then from the new types another types were derived, and so on. Today, ACM is rich enough to pay historians to study its history. One thing historians tried to find out is so called derivation plan -- i.e. how the truck types were derived. They defined the distance of truck types as the number of positions with different letters in truck type codes. They also assumed that each truck type was derived from exactly one other truck type (except for the first truck type which was not derived from any other type). The quality of a derivation plan was then defined as 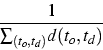where the sum goes over all pairs of types in the derivation plan such that to is the original type and td the type derived from it and d(to,td) is the distance of the types. Since historians failed, you are to write a program to help them. Given the codes of truck types, your program should find the highest possible quality of a derivation plan. Input Specification The input consists of several test cases. Each test case begins with a line containing the number of truck types, N, 2 N 2 000. Each of the following N lines of input contains one truck type code (a string of seven lowercase letters). You may assume that the codes uniquely describe the trucks, i.e., no two of these N lines are the same. The input is terminated with zero at the place of number of truck types. Output Specification For each test case, your program should output the text "The highest possible quality is 1/Q.", where 1/Q is the quality of the best derivation plan. Sample Input 4 aaaaaaa baaaaaa abaaaaa aabaaaa 0 Sample Output The highest possible quality is 1/3. Base Numbers numbers.c, numbers.p numbers.in.gz, numbers.out.gz numbers.ps.gz Any integer number can be written as a sequence of digits. The most popular system is decimal, which uses ten digits (its base is 10). Besides, other systems with different bases can be used. For instance, the binary system (with the base of 2) is often used in relation to computers. Generally, if we have a non-negative integer number n expressed as a sequence of digits dk dk-1 ...d2 d1 d0 in the system with the base r (r > 1), then the value of the number is n = dk rk + dk-1 rk-1 + ... + d2 r2 + d1 r + d0. Under any circumstances, each digit must be smaller than the base, 0 di < r for every i, 0 i k. Some problems arise when we use bases greater than 10, because then we need more than 10 popular digits. A common solution is to use letters for ``digits'' greater than 9. Although this solution pushes limits a little further, it does not avoid the problem itself -- the set of letters is still very limited. Thus, higher bases could not be used. Another solution is to write every digit separately as a number in the decimal system. For example, the hexadecimal number 1A8D (in usual notation) can be written as ``(1-10-8-13)16''. Please note that the number is always followed by the base value (even in the decimal system) to avoid misinterpretations. This number format is called a decimal-encoded notation in this text. A number in the decimal-encoded notation is considered valid only if it contains no unnecessary zeros, i.e., additional leading zeros cannot appear in the base value or in any of the digits. Moreover, all digits must always be smaller than the base value. Thus, ``(1-0-0-0)7'', ``(4-7689)7690'', and ``(0)16'' are valid decimal-encoded numbers, on the other hand, ``(0-3-6)8'', ``(1-02-3)6'', ``(3-2-1)07'', and ``(9)6'' are invalid. Due to some implementation reasons, ACM stores some data in valid decimal-encoded formats with various bases. Due to a software bug, a file containing a set of such numbers was damaged. All decimal digits has been preserved in the right order, but all of the dashes and parentheses were lost. Thus, each representation of a number was transformed to a code consisting of decimal digits only. Unfortunately, these codes are very ambiguous, most of them could represent many different numbers. For instance, ``1234'' could stand for ``(1-2-3)4'', ``(12)34'', ``(1-2)34'', or ``(1)234''. Your task is to determine the number of different representations that a code could stand for. Input Specification The input file consists of several lines. Each line contains one code, i.e., the string consisting of decimal digits. The maximum length of any code is 35, the minimum length is 1. The last line of the input file contains a single hash character ("#"). Output Specification For each code, output a single line of text. If there is no valid representation of a number resulting in the given code, print a single line containing the text "The code CCC is invalid.". Otherwise, print the text "The code CCC can represent X numbers.". Replace CCC with the given code. Replace X with the total number of different representations in the decimal-encoded notation that would result in the given code when dashes and parentheses are removed. Note that the representations of numbers are considered different even if they result in the same value. Sample Input 1234 102 201 123456 # Sample Output The code 1234 can represent 4 numbers. The code 102 can represent 1 numbers. The code 201 is invalid. The code 123456 can represent 13 numbers. Paper Cutting paper.c, paper.p paper.in.gz, paper.out.gz paper.ps.gz ACM managers need business cards to present themselves to their customers and partners. After the cards are printed on a large sheet of paper, they are cut with a special cutting machine. Since the machine operation is very expensive, it is necessary to minimize the number of cuts made. Your task is to find the optimal solution to produce the business cards. There are several limitations you have to comply with. The cards are always printed in a grid structure of exactly a b cards. The structure size (number of business cards in a single row and column) is fixed and cannot be changed due to a printing software restrictions. The sheet is always rectangular and its size is fixed. The grid must be perpendicular to the sheet edges, i.e., it can be rotated by 90 degrees only. However, you can exchange the meaning of rows and columns and place the cards into any position on the sheet, they can even touch the paper edges. For instance, assume the card size is 3 4 cm, and the grid size 1 2 cards. The four possible orientations of the grid are depicted in the following figure. The minimum paper size needed for each of them is stated. 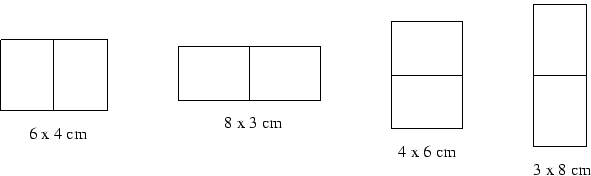The cutting machine used to cut the cards is able to make an arbitrary long continuous cut. The cut must run through the whole piece of the paper, it cannot stop in the middle. Only one free piece of paper can be cut at once -- you cannot stack pieces of paper onto each other, nor place them beside each other to save cuts. Input Specification The input consists of several test cases. Each of them is specified by six positive integer numbers, A,B,C,D,E,F, on one line separated by a space. The numbers are: A and B are the size of a rectangular grid, 1 A,B 1 000, C and D are the dimensions of a card in cms, 1 C,D 1 000, and E and F are the dimensions of a paper sheet in cms, 1 E,F 1 000 000. The input is terminated by a line containing six zeros. Output Specification For each of the test cases, output a single line. The line should contain the text: "The minimum number of cuts is X.", where X is the minimal number of cuts required. If it is not possible to fit the card grid onto the sheet, output the sentence "The paper is too small." instead. Sample Input 1 2 3 4 9 4 1 2 3 4 8 3 1 2 3 4 5 5 3 3 3 3 10 10 0 0 0 0 0 0 Sample Output The minimum number of cuts is 2. The minimum number of cuts is 1. The paper is too small. The minimum number of cuts is 10. 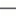Hexagonal Routes routing.c, routing.p routing.in.gz, routing.out.gz routing.ps.gz Finding the shortest route is the typical task of a truck driver. If the truck moves via the shortest route, it saves money. It is also important to know alternative routes of the same length, for the case a route is unavailable, e.g., due to some road work. To describe a region, we need to model a map of it. ACM recently found that triangular and rectangular based models are insufficient and decided to use hexagons for describing maps. Given a regular hexagonal grid (like honeycombs), we can number the cells starting with 1 (in any particular cell) and going in a spiral-like manner to other cells. This way, each cell is uniquely identified by its number and vice versa, each positive integer identifies a single cell. Two cells are called neighboring iff they have one side in common. In an infinite structure, each cell has exactly six neighbors. For instance, cell number 2 neighbors to cells 1, 3, 7, 8, 9 and 10. A hexagonal route is a non-empty sequence of cells where each cell in the sequence (except the last one) neighbors with its successor. A hexagonal route between two cells X and Y is a hexagonal route with X being the first member of the sequence, and Y being the last. The length of the route is the number of cells minus one. It represents the number of steps we need to make to travel via the route. Your task is to determine the length of the shortest possible route between two cells and the total number of mutually different routes of that length. Different routes must differ in at least one sequence member, i.e., they do not need to form completely disjoint sequences. Input Specification The input consists of a series of tasks, each of them given on one separate line. The line contains two integer numbers X and Y, separated by a space, 1 X, Y 1 000 000, X Y. These numbers identify two different cells. The last task is followed by a line containing two zeros. This line terminates the input. Output Specification For each task, output the sentence "There are N routes of the shortest length L.". Replace L with the smallest possible route length between cells X and Y. Replace N with the number of different routes of that length. If there is a single route only, use the words "is" and "route" instead of "are" and "routes". Sample Input 1 2 1 7 1 8 1 19 7 12 1000 9000 0 0 Sample Output There is 1 route of the shortest length 1. There is 1 route of the shortest length 1. There are 2 routes of the shortest length 2. There is 1 route of the shortest length 2. There are 3 routes of the shortest length 3. There are 278940769844931007968 routes of the shortest length 73. Storehouse store.c, store.p store.in.gz, store.out.gz store.ps.gz Advanced Cargo Movement, Ltd. owns a big storehouse in which a lot of various goods is stored. The storehouse has limited number of bays where a cargo can be loaded. Each day, trucks come to the bays, load their cargo (each truck loads just one type of goods) and leave for the shops. In order to speedup the loading, storekeepers move the goods to the bay in advance. Since the exact quantity of cargo to be loaded is not known beforehand, the storekeepers must prepare more goods than needed and the left-over goods is then returned to the store. Thus, it is useful when the next truck coming to the bay loads the same goods as the previous one, because it saves unnecessary movement of cargo. The capacity of trucks is much smaller than the capacity of the bay, therefore, any number of trucks can be served from one bay without reloading, as long as they want to load the same type of goods. Your task is to organize which type of goods will be prepared in which bay, so that storekeepers must move the unloaded goods back to the storehouse as few times as possible. At the beginning of each day, no goods is prepared in any bay. The goods left in bays at the end of the day is not counted to the number of moves needed. Input Specification The first line of the input contains the number of test cases to solve. Each test case starts with the line containing three integer numbers, B, G, N, 1 B 1 000, 1 G 1 000 000, 1 N 1 000 000, separated by a single space. B is the number of bays in the storehouse, G the number of types of goods stored in the storehouse and N the number of trucks coming to the storehouse. The test case continues by N lines. On the i-th line, there is a number ti, 1 ti G, specifying the type of goods the i-th truck wants to load. Output Specification For each test case, your program should output "Case X:" on the first line, where X is the case number starting with one. Then N lines follow. For each i, 1 i N, the i-th line must contain one of the following strings: "NO ACTION" -- when no action needs to be performed before the arrival of the truck i(i.e., the goods i-th truck wants to load is already at some bay), or "LOAD b g" -- when the goods with number g should be moved to the bay b before the i-th truck arrives. The goods currently present at the bay b is automatically moved back to the storehouse. Each time some truck arrives, the goods it wants to load must be prepared at some bay. Assume that any truck leaves the bay before the next one arrives, i.e., only a single truck is served at a time. The number of "LOAD" actions should be as small as possible. If there are more solutions with the same number of "LOAD" actions, choose any one you want. Outputs for different test cases should be separated by a blank line. Sample Input 2 2 4 5 1 2 1 4 1 3 3 3 1 3 2 Sample Output Case 1: LOAD 1 1 LOAD 2 2 NO ACTION LOAD 2 4 NO ACTION Case 2: LOAD 1 1 LOAD 2 3 LOAD 3 2 Traffic Jam traffic.c, traffic.p traffic.in.gz, traffic.out.gz traffic.ps.gz Traffic jam is a real nightmare of all drivers. Nobody likes to be stuck in the overfilled streets, when the cars move very slowly, if they even move at all. Professional drivers face traffic jams quite often. Truck drivers of ACM are not an exception. Can you help drivers to find the way out of the traffic jam? We can model a small (but complicated) traffic jam on a 6 6grid of squares. Vehicles (cars and trucks) are scattered over the grid at integer locations, as shown below. Both types of vehicles are 1 square wide. Cars are 2 squares long, and trucks are 3 squares long. Vehicles may be oriented either horizontally (East-West) or vertically (North-South) relative to the grid. 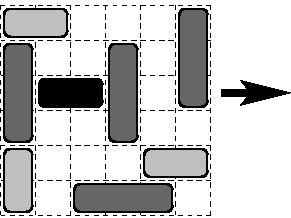Vehicles cannot move through each other, cannot turn, and cannot move over the edge of the grid. They can move in their direction (horizontally-oriented vehicles cannot move vertically and vice versa), as long as they are not blocked by another vehicle or by the edge of the grid. Only one vehicle may move in a single step, but it may move by as many squares at a time as possible, providing there is enough empty space. Our goal is to move vehicles back and forth until a particular horizontally-oriented vehicle (your own car -- the black one on the picture above) leaves the rightmost (eastern-most) edge of the grid, where it is considered to have escaped the traffic jam. You are to write a program that will find a solution requiring the minimum possible number of moves. Input Specification The input file will consist of one or more input scenarios. Each scenario begins with a single integer n, 1 n 10, giving the number of vehicles in the scenario. Then there will be 6 lines of input, each containing 6 characters. Each character is either a dot (".") representing an empty square, or a lowercase letter representing a vehicle. Your own vehicle is always oriented horizontally and represented by "x" characters. The other vehicles use the letters sequentially, beginning with "a". The last scenario will be followed by a line containing a single zero. Output Specification For each scenario, output a single line with the statement "Scenario #K requires X moves.", where K is the number of the scenario (starting with 1) and X is the minimum number of moves required to escape the the traffic jam with the particular car. If it is not possible to escape, output the sentence "You are trapped in scenario #K." instead. Sample Input 8 aa...b c..d.b cxxd.b c..d.. e...ff e.ggg. 8 abbc.. a..c.. axxc.. ..gddd ..g..e ..fffe 0 Sample Output Scenario #1 requires 8 moves. Scenario #2 requires 25 moves.