|  |
|
Czech ACM Student Chapter
CTU in Prague, Dept. of Computer Science and Engineering V©B TU Ostrava, FEI, Dept. of Computer Science SUT Bratislava, FEI, Dept. of Computer Science and Engineering CTU Open Contest 2002Dear contestants:As you probably know, NATO Summit will be held in Prague in the end of November 2002. This important event brings many challenging problems that must be solved to ensure the safety and convenience of all participants. Many of such problems can be solved with the help of computers, if we have a proper software equipment. Fortunately, the people in Summit Headquarters know very well who can develop programs for solving these complex tasks. They know that the best programmers participate in the CTU Open Contest every year. Therefore, they asked us to give you descriptions of the most important problems. You are to solve them now. Note that the success of this big international event depends on you. All of the programs will run in UNIX environment. Every program should read data from the standard input and send results to the standard output. The data format is given and must be exactly followed. There will be no extra spaces in the input and there should be no extra spaces and newlines in the output, if not stated otherwise. The end-of-line character is not considered a part of the line. All numbers will fit into the standard signed integer type of 32 bits, if the description of a particular problem does not say otherwise. We wish you a lot of fun and good luck with solving these problems. The reputation of the Czech Republic is in your hands. And please remember: this mission is top secret! You must not tell anyone you were here. ;-) Your organizing team
intro.ps
The problems have been taken from the following sources:
Sea Battle
During the Summit, the armed forces will be highly active. The police will monitor Prague streets, the army will guard buildings, the Czech air space will be full of American F-16s. Moreover, the ships and battle cruisers will be sent to guard the banks of the Vltava river. Unfortunately, in the case of any incident, the Czech Admiralty have only a few captains able to control over the large sea battle. Therefore, it was decided to educate new admirals. As an excellent preparation, the game of "Sea Battle" was chosen to help with their study program. In this well-known game, a predefined number of ships of predefined shapes are placed on the square board in such a way that they cannot contact one another even with their corners. In this task, we will consider rectangular shaped ships only. The unknown number of rectangular ships of unknown sizes are placed on a rectangular board. All the ships are full rectangles built of hash characters. Write a program that counts the total number of ships present in the field.
Input Specification
The input consists of more scenarios. The description of each scenario begins
with two integer numbers R and C separated with a single space,
1 After these two numbers, there are R lines, each of them containing C characters. Each character is either hash ("#") or dot ("."). Hashes denote ships, dots water. Then, the next scenario description begins. At the end of the input, there will be a line containing two zeros instead of the field size.
Output SpecificationOutput a single line for every scenario. If the ships were placed correctly (i.e., there are only rectangles that do not touch each other even with a corner), print the sentence "There are S ships." where S is the number of ships. Otherwise, print the sentence "Bad placement.".
Sample Input6 6 .....# ##...# ##...# ..#..# .....# ###### 6 8 .....#.# ##.....# ##.....# .......# #......# #..#...# 0 0
Output for Sample InputBad placement. There are 5 ships.
The Die Is Cast
According to a usually reliable source (that does not want to be published), the dangerous anarchist group New Tomorrow (aka NT 2000) prepares a frontal attack against the Congress Center. The anarchists had big troubles choosing the proper moment to begin with their attack. Finally, they have agreed upon to let the fortune decide. They are going to play dice (which is, moreover, good thing to have fun while waiting for the action) and when six dots appear on the top side of all dice, it is the signal to begin the attack. The police knows that and they want to be informed about the signal. Fortunately, the area around the Congress Center is monitored with cameras. Thus, the police can have the picture of the anarchists in any given moment during their play. To automate the processing, they need a program that gets the bitmap image and determines the outcome of the throw that has just been performed, i.e., the the number of dots visible on each die. We make the following assumptions about the input images. The images contain only three different pixel values: for the background, the dice and the dots on the dice. We consider two pixels connected if they share an edge -- meeting at a corner is not enough. In the figure, pixels A and B are connected, but B and C are not.

A set S of pixels is connected if for every pair a,b of pixels in S,
there is a sequence a1, a2, ... ak in S such that a = a1,
b = ak, and for any 1 We consider all maximally connected sets consisting solely of non-background pixels to be dice. "Maximally connected" means that you cannot add any other non-background pixels to the set without making it disconnected. Likewise, we consider every maximal connected set of dot pixels to form a dot.
Input Specification
The input consists of pictures of several dice throws. Each picture
description starts with a line containing two numbers H and W, the height
and width of the picture, respectively, 1 The following H lines contain W characters each. The characters can be: dot (".") for a background pixel, asterisk ("*") for a pixel of a die, and "X" for a pixel of a die's dot. The picture will contain at least one die, and the numbers of dots per die is between 1 and 6, inclusive. The maximal number of dice in the picture is limited only by its size. Dice and dots may have different sizes and may not be entirely square due to optical distortion. In fact, they can have arbitrary shape, as far as they remain connected. Anyway, you can assume the dice cannot be "hollow", i.e., if we consider all the pixels outside the picture to be background, all background pixels are connected. The input is terminated by a picture starting with w = h = 0, which should not be processed.
Output SpecificationFor each throw of dice, output a single line containing the text "Throw:" followed by a space and the number of dots on all the dice in the picture, sorted in increasing order. Numbers should be separated with a single space.
Sample Input15 30 .............................. ................*............. ...*****.......****........... ...*X***......**X***.......... ...*****.....***X**........... ...***X*......****............ ...*****........*............. .............................. .............................. .....***.........******....... ....**X****......*X**X*....... ...*******.......******....... ..****X**........*X**X*....... .....***.........******....... .............................. 3 3 ... XXX ... 0 0
Output for Sample InputThrow: 1 2 2 4 Throw: 1
Defragmentation
For the maximal security, the special secure operation system is used in the Summit Headquarters. This OS uses also the special file system. In this file system all disk space is divided into N clusters of equal sizes, numbered by integers from 1 to N. Each file occupies one or more clusters in arbitrary areas of the disk. All clusters that are not occupied by files are considered to be free. A file can be read from the disk in the fastest way, if all its clusters are situated in the successive disk clusters in the natural order. Rotation of the disk with constant speed implies that various amounts of time are needed for accessing its clusters. Therefore, reading of clusters located near the beginning of the disk performs faster than reading of the ones located near its end. Thus, all files are numbered beforehand by integers from 1 to K in the order of descending frequency of access. Under the optimal placing of the files on the disk the file number 1 will occupy clusters 1, 2, ..., S1, the file number 2 will occupy clusters S1 + 1, S1 + 2, ..., S1 + S2 and so on (Si is the number of clusters occupied by the i-th file). In order to place the files on the disk in the optimal way, cluster-moving operations are executed. One cluster-moving operation includes reading of one occupied cluster from the disk to the memory and writing its contents to some free cluster. After that, the first cluster is declared free, and the second one is declared occupied. Your goal is to place the files on the disk in the optimal way by executing the minimal possible number of cluster-moving operations.
Input Specification
The input consists of several disk descriptions. The first line of the
description contains two integers N and K separated by a space,
1 All cluster numbers in one disk description are different and there is always at least one free cluster on the disk. The input is terminated with the line containing two zeros in place of numbers N and K.
Output SpecificationFor each disk description, output exactly one line containing the sentence "We need M move operations." where M is the minimal number of cluster-moving operations needed to place the files on the disk into the optimal clusters. If the files on the disk are already placed in the optimal way, the output should only contain the sentence "No optimization needed.".
Sample Input20 3 4 2 3 11 12 1 7 3 18 5 10 30 4 2 1 2 3 3 4 5 2 6 7 8 8 9 10 11 12 13 14 15 0 0
Output for Sample InputWe need 9 move operations. No optimization needed.
Formatting Text
Writing e-mails is fun, but, unfortunately, they often do not look very nice, mainly because not all lines have the same lengths. Summit representatives want to sent nicely formatted e-mails and your task is to write an e-mail formatting program for them. The easiest way to perform this task would be to insert more spaces between the words in lines which are too short. But this is not the best way. Consider the following example:
**************************** This is the example you are actually considering. Let us assume that we want to get lines as long as the row of stars. Then, by simply inserting spaces, we would get
**************************** This is the example you are actually considering. But this looks rather odd because of the large gap in the second line. By moving the word "are" from the first to the second line, we get a better result:
**************************** This is the example you are actually considering. Of course, this has to be formalized. To do this, we assign a badness to each gap between words. The badness assigned to a gap of n spaces is (n-1)2. The goal of the program is to minimize the sum of all badnesses. For example, the badness of the first example is 1 + 72 = 50, whereas the badness of the second one is only 1 + 1 + 1 + 4 + 1 + 4 = 12. In the output, every line should start and end with a word. I.e., there cannot be a gap at the beginning or at the end of a line. The only exception to this are the lines that contain a single word only. You can output such lines provided that the word is put at the beginning of the line. A badness of 500 is assigned to such a line if it is shorter than it should be. Of course, in this case, the length of the line is simply the length of the single word.
Input Specification
The input file contains a text consisting of several paragraphs. Each
paragraph is preceded by a line containing a single integer N, the desired
width of the paragraph, 1 Each paragraph is terminated by exactly one blank line. There is no limit on the number of paragraphs in the input file. The input file will be terminated by a paragraph description starting with N = 0. This paragraph should not be processed.
Output SpecificationFor each paragraph, find the formatting with the lowest possible badness and output the sentence "Minimal badness is B." where B is the badness of the best possible formatting.
Sample Input28 This is the example you are actually considering. 25 Writing e-mails is fun, and with this program, they even look nice. 0
Output for Sample InputMinimal badness is 12. Minimal badness is 14.
Hole Cutter
The assistants of Summit Headquarters often need to cut various shapes from the large sheet of paper. For instance, they want to distribute posters of various sizes etc. They have just acquired a new cutter which can make cuts much more freely than any of their previous machines, and they want you to write a program to calculate exactly what happens when a complex series of cuts are made. In particular, they need to know the number of holes which are formed in the sheet by the cuts. The pictures show some examples of situations that can arise after cutting.
Input Specification
The input consists of several operation descriptions. Each description starts
with a line containing an integer number N, giving the number of cuts in
the operation, 1 You should assume the points are always internal to the sheet, never on the boundary. Each cut will be parallel to the x- or y-axis of the table. The input will be terminated by a line consisting of a single 0, i.e. a cutting operation description with N = 0.
Output SpecificationFor each cutting operation, output a single line containing the sentence "There are H holes." where H is the number of distinct holes in the sheet after all the cuts have been made. Note that the minimum area of any hole is 1 square unit.
Sample Input
Output for Sample Input
Interesting Maze Game
The Police President has recently bought a new game -- the famous Ravensburger's aMAZEing Labyrinth. Now, he is really keen on it, he spends any free time playing this game. While we want the Police President during the Summit to perform much more important decisions, we need a program that would substitute him in playing the game.
The game is played on the field of 7
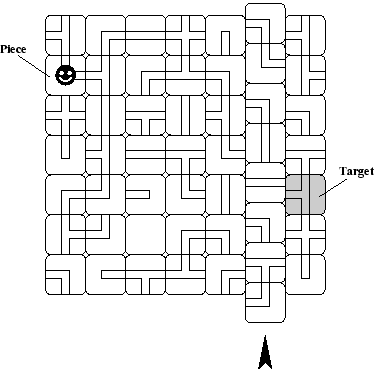
In the beginning of the move, the player has one game piece on some of the square cards and his/her goal is to move the piece to some other square card (target) following the valid paths. Before the walk, the player alters the maze state by inserting one extra square card into it. The extra card can only be inserted to the position at the field margin. The insertion causes the whole row or column of cards to be shifted one position further, which makes another card to fall out at the other end of the game field. (This card becomes a new extra card for the next move, but we will care of a single move only in this problem.)
Since the cards with both coordinates odd are stuck firmly to the playing
desk, only the even rows and columns can be shifted. Thus, the extra card
can be inserted into an even row or column only. If we number rows and
columns with numbers 1 to 7, there are 12 possible positions where the new
card can be inserted: (1,2), (1,4), (1,6), (7,2), (7,4), (7,6),
(2,1), (4,1), (6,1), (2,7), (4,7), and (6,7). For instance,
insertion into the position (7,6) causes the following shift:
(7,6)
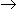 (6,6) (6,6) 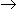 (5,6) (5,6) 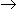 (4,6) (4,6)
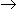 (3,6) (3,6)  (2,6) (2,6)  (1,6) (1,6)
The extra card comes to the position (7,6) and the card formerly being at the position (1,6) is removed from the game field for the rest of the move. Before insertion, the extra card can be rotated to any of the four possible directions. No other card in the game can be rotated. This makes the total maximal number of 48 possible moves (if the extra card is asymmetric). Another important rule considers the case when the target card or the card with the player's piece appears in the row or column being shifted. In such case, the position of the piece or the target is shifted too. This makes it possible to move the target to some more appropriate place. Note that if the target is shifted away from the game (the target card falls out from the game), it is no more possible to reach it in the same move -- the piece cannot leave the game field. On the other hand, if the game piece is located on the card which is moved away from the game field, the piece position is "wrapped" to the opposite end of the field, i.e., to the just inserted card. Therefore, a valid move consists of two parts: insertion of the extra card into the game (this action must always be made) and walking the path of an arbitrary length (including zero, i.e., staying on the same square). Your task is to determine, whether it is possible to reach the target in a single move. In other words, if it is possible to insert the extra card into the game and then to walk to the target position.
Input Specification
The input consists of several game descriptions. The first line of each
description contains four integer numbers R1, C1, R2, and C2separated with a space, 1
The next three lines describe the first row of the game field. Each of these
lines contains 27 characters: three for the card in the first column, one
space, three characters for the card in the second column, etc. Thus, every
card is represented by a square of nine (3 After the first row, there is one blank line and three other lines describing the second row. Then follow one other blank line and three lines for the third row, etc. After the seventh row, there is a blank line and three other lines containing exactly three characters each. This is the description of the extra card, given in the same way as the cards in the field. The input is terminated by a line containing four zeros instead of piece and target coordinates.
Output SpecificationFor each game, output a single line. If it is possible to insert the extra card in such a way that there is a path from the game piece to the target, print the sentence "You can win in one move.". Otherwise, print the sentence "Bad luck!".
Sample Input1 1 7 7 ... ... ... .|. ... ... ... -O- -O- -O- .O. -O- -O- -O. ... ... ... .|. ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... ... .|. .O. .|. 1 1 7 7 ... ... ... ... ... ... ... -O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... .|. ... ... ... ... ... ... .|. .O- -O- -O- -O- -O- -O- -O. .|. ... ... ... ... ... ... .|. ... ... ... ... ... ... .O- -O- -O- -O- -O- -O- -O. ... ... ... ... ... ... ... ... .O- .|. 0 0 0 0
Output for Sample InputYou can win in one move. Bad luck!
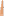    
Complicated Route
The Prague citizens are preparing for the Summit too. Most importantly, they must be prepared for limited possibilities of movement through the city. The Home Affairs Department issued ten recommendations how to behave (so called "decalogue"). One of these points says to obey the directions of the police, even if they recommend more complicated routes to the place a person wants to walk to. The directions describing the route usually tell us something like "Start at this corner. Take three steps towards the tall chimney, then seventeen steps towards the small maple tree, ... blah blah ..., finally six steps towards the graffiti painting. Then you will be there." Most of these directions just boil down to taking the mentioned number of steps in one of the eight principal compass directions (depicted in the figure).
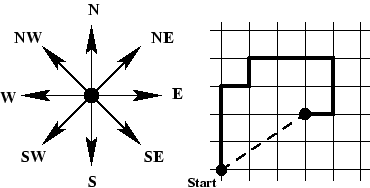
Obviously, following the paths given by the police may lead to an interesting tour of the local scenery, but if one is in a hurry, there is usually a much faster way: just march directly from your starting point to the place where you want to go. Instead of taking three steps north, one step east, one step north, three steps east, two steps south and one step west (see figure) following the direct route (dashed line in figure) will result in a path of about 3.6 steps. You are to write a program that computes the location of and distance to the target place, given a recommended route.
Disclaimer: Note that this contest problem assignment is not a challenge to violate the police recommendations! We take no responsibility for any improper use of the program.
Input SpecificationThe input file contains several strings, each one on a line by itself, and each one consisting of at most 200 characters. The last string will be "END", signaling the end of the input. All other strings describe one route, according to the following format: The description is a comma-separated list of pairs of lengths (positive integers less than 10000) and directions: "N" (north), "NE" (northeast), "E" (east), "SE" (southeast), "S" (south), "SW" (southwest), "W" (west), or "NW" (northwest). For example, "3W" means 3 steps to the west, and "17NE" means 17 steps to the northeast. A fullstop (".") terminates the description, which contains no blanks.
Output SpecificationFor every map description in the input, output a single line containing the sentence "You can go to (X,Y), the distance is D steps." where X and Y are the absolute coordinates of the target point of the route. The coordinate system is oriented such that the x-axis points east, and the y-axis points north. The path always starts at the origin (0,0). The fractional values X, Y, and D must be printed exact to three digits to the right of the decimal point.
Sample Input3N,1E,1N,3E,2S,1W. 10NW. END
Output for Sample InputYou can go to (3.000,2.000), the distance is 3.606 steps. You can go to (-7.071,7.071), the distance is 10.000 steps.
The Perfect Symmetry
The representatives of NATO countries must be guarded by many bodyguards during the Summit. Each V.I.P. is accompanied by his own bodyguards but is also assigned many other specialists, snipers, etc. To make their work efficient and the guarded person secure as much as possible, the bodyguards must be distributed to various directions from the person. The optimal placement of bodyguards is such that the V.I.P. stands in the center of symmetry of all guards. Unfortunately, when the V.I.P. moves, it is very hard to reconfigure the bodyguards' positions to reflect the new situation. Most of the Czech specialists are not able to do such reconfigurations in real-time. Therefore, the Home Affairs Minister Sobeslav Gros has decided to reverse this procedure. The bodyguards take their places first. Then, it is the responsibility of the V.I.P. to find the proper position in the center of symmetry. If the person appears anywhere else, we take no responsibility for his/her security.
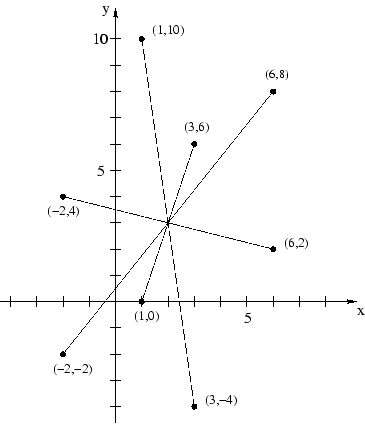
Your task is to automate the process. Given a set of N points (bodyguard positions), you are to find its center of symmetry S, where the V.I.P. is relatively safe. More formal description follows. Let's have a point A and the center of symmetry S. We say that another point A' is the image of the point A according to the center of symmetry S iff S is the center of the line joining points A and A'. The image of the set of points (X) according to the center S is the set of all images of individual points in that set. The set X is said to possess a center of symmetry, if there exists a point S such that the image of the set X according to the center S is equal to the set X itself.
Input Specification
The input consists of several assignments. Each assignment begins with
a line containing a single integer number N, 1 Since no two bodyguards occupy the same place, no point will appear twice in the same assignment. However, note that a bodyguard can be in the same place as the V.I.P. After the last assignment, there is a line containing zero instead of the number of points. This line should not be processed.
Output SpecificationFor each assignment, output exactly one line. If the given set possesses a center of symmetry, print the text "V.I.P. should stay at (X,Y)." where X and Y are the Cartesian coordinates of the center rounded to the nearest number with exactly one digit after the decimal point. If there is no center of symmetry, output the text: "This is a dangerous situation!".
Sample Input8 1 10 3 6 6 8 6 2 3 -4 1 0 -2 -2 -2 4 4 2 1 4 1 5 1 6 1 0
Output for Sample InputV.I.P. should stay at (2.0,3.0). This is a dangerous situation!
Mysterious Villa
Mr. Black is an advisor of the Turkish president and as such, he is going to come to the NATO Summit. He likes to live alone, far from the official Summit hotels. Therefore, he rented a big villa in Orechovka. Only one thing bothers him: although there are light switches in most rooms, the lights they control are often in other rooms than the switches themselves. While his estate agent saw this as a feature, Mr. Black has come to believe that the electricians were a bit absent-minded (to put it mildly) when they connected the switches to the outlets. Some nights, Mr. Black will come home late. While standing in the hallway, the lights in all other rooms are switched off. Unfortunately, Mr. Black is afraid of the dark, so he never dares to enter a room that had its lights out and would never switch off the lights of the room he was in. Mr. Black wants to use the incorrectly wired light switches to his advantage. He should manage to get to his bedroom and to switch off all lights except for the one in the bedroom. You are to write a program that, given a description of a villa, determines how to get from the hallway to the bedroom if only the hallway light is initially switched on. You may never enter a dark room, switch off the light in the room you are just in, and after the last move, all lights except for the one in the bedroom must be switched off. If there are several paths to the bedroom, you have to find the one which uses the smallest number of steps, where "move from one room to another", "switch on a light" and "switch off a light" each counts as one step.
Input Specification
The input file contains several villa descriptions. Each villa starts with
a line containing three integers R, D, and S.
R is the number of rooms in the villa, 1 This line is followed by D lines containing two integers I and J each, specifying that room I is connected to room J by a door. Then follow S lines containing two integers K and L each, indicating that there is a light switch in room K that controls the light in room L. A blank line separates the villa description from the next one. The input file ends with a villa having R = D = S = 0, which should not be processed.
Output SpecificationFor each villa, output a single line. If there is a solution to Mr. Black's problem, output the sentence "Mr. Black needs X steps." where X is the minimal number of steps that lead him to his bedroom and only leave the bedroom light switched on. If there is no solution, output the statement "Poor Mr. Black! No sleep tonight!".
Sample Input3 3 4 1 2 1 3 3 2 1 2 1 3 2 1 3 2 2 1 2 2 1 1 1 1 2 0 0 0
Output for Sample InputMr. Black needs 6 steps. Poor Mr. Black! No sleep tonight!
Too Much Water
Fred Mapper is a real estate agent in Prague. Many foreign delegates participating in NATO Summit ask him to find some house for them, because they want to rent it during their stay in Prague. Some even plan to stay here for a longer time after the Summit ends. Unfortunately, many of them saw the pictures on TV showing the floods that happened in August, and are afraid of water. Many of Fred's properties are located in Kampa. In the process of investigating the August data, he learned that in the case of flooding, the water covers exactly 50 square meters each hour. Now we need to know how much time is available for evacuation in any given point.
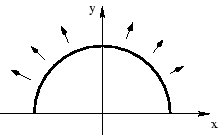
After doing more research, Fred has learned that the land that is being flooded forms a semicircle. This semicircle is part of a circle centered at (0,0), with the line that bisects the circle being the x-axis. Locations below the x-axis are in the river. The semicircle has an area of 0 at the beginning of hour 1 (when the flood begins). The semicircle is illustrated in the Figure.
Input Specification
The line consists of several property descriptions. Each property is
described by one line containing two numbers X and Y which are the
Cartesian coordinates of the property. X and Y are floating point numbers
measured in meters and given with one digit after the decimal point,
-1000 The point (0,0) will not be given with the exception of the last line, where two zeros are given to terminate the input. This last line should not be processed.
Output SpecificationFor each property, a single line of output should appear. This line should take the form of "The property will be flooded in hour Z." where Zis the first hour (counted from 1) this property will be within the semicircle at the end of hour Z. Z must be an integer. No property will appear exactly on the semicircle boundary at the end of any hour, it will either be inside or outside.
Sample Input1.0 1.0 25.0 0.0 0 0
Output for Sample InputThe property will be flooded in hour 1. The property will be flooded in hour 20.
|
 R,C
R,C 
 7 squares with equal-sized
cards lying on each square. Various path patterns are drawn on the cards,
these paths join arbitrary subset of the four edges of a single square.
The patterns can form longer paths leading through the whole game field.
When following these paths, it is possible to move from a square to its
neighbouring square, if both squares contain the path pattern leading to
their common edge. It is impossible to travel between squares diagonally.
See the picture for a better idea about the game appearance.
7 squares with equal-sized
cards lying on each square. Various path patterns are drawn on the cards,
these paths join arbitrary subset of the four edges of a single square.
The patterns can form longer paths leading through the whole game field.
When following these paths, it is possible to move from a square to its
neighbouring square, if both squares contain the path pattern leading to
their common edge. It is impossible to travel between squares diagonally.
See the picture for a better idea about the game appearance.