|  |
|
The problems have been taken from the following sources:
Oh, Those Achin' Feet2001 Mid-Atlantic Regional Contest
In recent days, a number of people have been injured after being pushed off the sidewalks due to overcrowding. City Hall is interested in figuring out how much pedestrian traffic its sidewalks receive every day. The results of this study will be used to determine whether the city needs to fund more sidewalks. The city has surveyed various buildings in several blocks to determine the traffic patterns they generate. Your job is to take this survey data and convert it into sidewalk utilization information. Your program will read in the size of the map and a map of several city blocks. Buildings, streets, and building entrance/exits will be marked on the map. You will also be given a list of pedestrian load between several pairs of exits and entrances. Your program will determine the paths used by pedestrians between each source and destination, add up the total pedestrian load from all paths using each street, and output a table of the total pedestrian load on each square.
Notes
Input Specification
Line 1: X Y
Lines 2-(Y+1):
Lines (Y+2)-?:
The test case will terminate with the line:
Output SpecificationThe output consists of Y lines, each with X space-separated fields indicating the load factor. Each load factor is printed to two decimal places with 3 spaces for integer digits (C 6.2 format).
Sample Input4 4 .... A.X. XXX. B... AB 2 BA 1 XX 0 0 0
Sample Output1.50 3.00 3.00 3.00 0.00 1.50 0.00 3.00 0.00 0.00 0.00 3.00 0.00 3.00 3.00 3.00
Cable Master2001 North-Eastern European Regional Contest Inhabitants of the Wonderland have decided to hold a regional programming contest. The Judging Committee has volunteered and has promised to organize the most honest contest ever. It was decided to connect computers for the contestants using a ``star'' topology - i.e. connect them all to a single central hub. To organize a truly honest contest, the Head of the Judging Committee has decreed to place all contestants evenly around the hub on an equal distance from it. To buy network cables, the Judging Committee has contacted a local network solutions provider with a request to sell for them a specified number of cables with equal lengths. The Judging Committee wants the cables to be as long as possible to sit contestants as far from each other as possible. The Cable Master of the company was assigned to the task. He knows the length of each cable in the stock up to a centimeter, and he can cut them with a centimeter precision being told the length of the pieces he must cut. However, this time, the length is not known and the Cable Master is completely puzzled. You are to help the Cable Master, by writing a program that will determine the maximal possible length of a cable piece that can be cut from the cables in the stock, to get the specified number of pieces.
Input Specification
The first line of the input file contains two integer numbers
N and K, separated by a space. N
(1 Then, a next test case follows. The input is terminated by two zeros.
Output SpecificationWrite to the output file the maximal length (in meters) of the pieces that Cable Master may cut from the cables in the stock to get the requested number of pieces. The number must be written with a centimeter precision, with exactly two digits after a decimal point. If it is not possible to cut the requested number of pieces each one being at least one centimeter long, then the output file must contain the single number ``0.00'' (without quotes).
Sample Input4 11 8.02 7.43 4.57 5.39 0 0
Sample Output2.00
Human Gene Functions2001 Asian Regional Contest -- Taejon Division It is well known that a human gene can be considered as a sequence, consisting of four nucleotides, which are simply denoted by four letters, A, C, G, and T. Biologists have been interested in identifying human genes and determining their functions, because these can be used to diagnose human diseases and to design new drugs for them. A human gene can be identified through a series of time-consuming biological experiments, often with the help of computer programs. Once a sequence of a gene is obtained, the next job is to determine its function. One of the methods for biologists to use in determining the function of a new gene sequence that they have just identified is to search a database with the new gene as a query. The database to be searched stores many gene sequences and their functions -- many researchers have been submitting their genes and functions to the database and the database is freely accessible through the Internet. A database search will return a list of gene sequences from the database that are similar to the query gene. Biologists assume that sequence similarity often implies functional similarity. So, the function of the new gene might be one of the functions that the genes from the list have. To exactly determine which one is the right one another series of biological experiments will be needed. Your job is to make a program that compares two genes and determines their similarity as explained below. Your program may be used as a part of the database search if you can provide an efficient one. Given two genes AGTGATG and GTTAG, how similar are they? One of the methods to measure the similarity of two genes is called alignment. In an alignment, spaces are inserted, if necessary, in appropriate positions of the genes to make them equally long and score the resulting genes according to a scoring matrix. For example, one space is inserted into AGTGATG to result in AGTGAT-G, and three spaces are inserted into GTTAG to result in GT-TAG. A space is denoted by a minus sign (-). The two genes are now of equal length. These two strings are aligned:
In this alignment, there are four matches, namely, G in the second position, T in the third, T in the sixth, and G in the eighth. Each pair of aligned characters is assigned a score according to the following scoring matrix.
* denotes that a space-space match is not allowed. The score of the alignment above is (- 3) + 5 + 5 + (- 2) + (- 3) + 5 + (- 3) + 5 = 9. Of course, many other alignments are possible. One is shown below (a different number of spaces are inserted into different positions):
This alignment gives a score of (- 3) + 5 + 5 + (- 2) + 5 + (- 1) + 5 = 14. So, this one is better than the previous one. As a matter of fact, this one is optimal since no other alignment can have a higher score. So, it is said that the similarity of the two genes is 14.
Input SpecificationThe input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case consists of two lines: each line contains an integer, the length of a gene, followed by a gene sequence. The length of each gene sequence is at least one and does not exceed 100.
Output SpecificationThe output should print the similarity of each test case, one per line.
Sample Input2 7 AGTGATG 5 GTTAG 7 AGCTATT 9 AGCTTTAAA
Sample Output14 21
Frame Stacking2001 Southern African Regional Contest
Consider the following 5 picture frames placed on an 9×8 array.
Now place them on top of one another starting with 1 at the bottom and ending up with 5 on top. If any part of a frame covers another it hides that part of the frame below. Viewing the stack of 5 frames we see the following.
In what order are the frames stacked from bottom to top? The answer is EDABC. Your problem is to determine the order in which the frames are stacked from bottom to top given a picture of the stacked frames. Here are the rules:
Input Specification
Each input block contains the height, h
(h Your input may contain multiple blocks of the format described above, without any blank lines in between. All blocks in the input must be processed sequentially. The file is terminated by two zeros in place of the dimensions.
Output SpecificationWrite the solution to the standard output. Give the letters of the frames in the order they were stacked from bottom to top. If there are multiple possibilities for an ordering, list all such possibilities in alphabetical order, each one on a separate line. There will always be at least one legal ordering for each input block. List the output for all blocks in the input sequentially, without any blank lines (not even between blocks).
Sample Input9 8 .CCC.... ECBCBB.. DCBCDB.. DCCC.B.. D.B.ABAA D.BBBB.A DDDDAD.A E...AAAA EEEEEE.. 0 0
Sample OutputEDABC
Number Game2001 North-Western Europe Regional Contest Christiane and Matthias are playing a new game, the Number Game. The rules of the Number Game are: Christian and Matthias take turns in choosing integer numbers greater than or equal to 2. The following rules restrict the set of numbers which may be chosen:
The player who cannot choose any number anymore looses the Number Game. Here is an example: Matthias starts by choosing 4. Then Christiane is not allowed to choose 4, 8, 12, etc. Let us assume her move is 3. Now, the numbers 3, 6, 9, etc. are excluded, too; furthermore, numbers like: 7 = 3 + 4, 10 = 2.3 + 4, 11 = 3 + 2.4, 13 = 3.3 + 4, ... are not available. So, in fact, the only numbers left are 2 and 5. Matthias now says 2. Since 5 = 2 + 3 is now forbidden, too, he wins because there is no number for Christiane s move left. Your task is to write a program which will help to play the Number Game. In general, i.e., without rule R3, this game may go on forever. However, with rule R3, it is possible to write a program that finds a strategy to win the game.
ProblemGiven a game situation (a list of numbers which are not yet forbidden), your program should output all winning moves. A winning move is a move by which the player whose turn it is can force a win no matter what the other player will do. Now we define these terms more formally:
Input SpecificationThe first line contains the number of scenarios.
The input for each scenario describes a game position. It begins with a line
containing the number a,
0 You may assume that all game positions in the input could really occur in the Number Game (for example, if 3 is not in the list of numbers available, 6 will not be, either).
Output SpecificationThe output for each scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. In the next line either print "There is no winning move." if this is true for the position of the current scenario, or "The winning moves are: w1 w2 ... wk." where the wi are all the winning moves, in ascending order, separated by single blanks. The output for each scenario should be followed by a blank line.
Sample Input2 1 2 2 2 3
Sample OutputScenario #1: The winning moves are: 2. Scenario #2: There is no winning move.
Number That Count1998 East Central Regional Contest
``Kronecker's Knumbers'' is a little company that manufactures plastic digits for use in signs (theater marquees, gas station price displays, and so on). The owner and sole employee, Klyde Kronecker, keeps track of how many digits of each type he has used by maintaining an inventory book. For instance, if he has just made a sign containing the telephone number "5553141", he'll write down the number ``5553141'' in one column of his book, and in the next column he'll list how many of each digit he used: two 1s, one 3, one 4, and three 5s. (Digits that don't get used don't appear in the inventory.) He writes the inventory in condensed form, like this: ``21131435''. The other day, Klyde filled an order for the number 31123314 and was amazed to discover that the inventory of this number is the same as the number -- it has three 1s, one 2, three 3s, and one 4! He calls this an example of a ``self-inventorying number'', and now he wants to find out which numbers are self-inventorying, or lead to a self-inventorying number through iterated application of the inventorying operation described below. You have been hired to help him in his investigations.
Given any non-negative integer n, its inventory is another integer
consisting of a concatenation of integers
c1d1c2d2...ckdk,
where each ci and di is an
unsigned integer, every ci is positive, the di satisfy
0
An integer n is called self-inventorying if n equals its inventory. It is
called self-inventorying after j steps
(j
Finally, n enters an inventory loop of length k
(k Write a program that will read a sequence of non-negative integers and, for each input value, state whether it is self-inventorying, self-inventorying after j steps, enters an inventory loop of length k, or has none of these properties after 15 iterative applications of the inventory function.
Input SpecificationA sequence of non-negative integers, each having at most 80 digits, followed by the terminating value -1. There are no extra leading zeros.
Output SpecificationFor each non-negative input value n, output the appropriate choice from among the following messages (where n is the input value, j is a positive integer, and k is a positive integer greater than 1):
Sample Input22 31123314 314213241519 21221314 111222234459 -1
Sample Output22 is self-inventorying 31123314 is self-inventorying 314213241519 enters an inventory loop of length 2 21221314 becomes self-inventorying after 2 steps 111222234459 enters an inventory loop of length 2
Spell Checker1998 North-Eastern European Regional Contest You, as a member of a development team for a new spell checking program, are to write a module that will check the correctness of given words using a known dictionary of all correct words in all their forms. If the word is absent in the dictionary then it can be replaced by correct words (from the dictionary) that can be obtained by one of the following operations:
Your task is to write the program that will find all possible replacements from the dictionary for every given word.
Input SpecificationThe first part of the input contains all words from the dictionary. Each word occupies its own line. This part is finished by the single character "#" on a separate line. All words are different. There will be at most 10000 words in the dictionary. The next part of the input contains all words that are to be checked. Each word occupies its own line. This part is also finished by the single character "#" on a separate line. There will be at most 50 words that are to be checked. All words in the input file (words from the dictionary and words to be checked) consist only of small alphabetic characters and each one contains 15 characters at most. The file may consist of more test cases. It is terminated by an empty dictionary.
Output SpecificationWrite to the output file exactly one line for every checked word in the order of their appearance in the second part of the input file. If the word is correct (i.e. it exists in the dictionary) write the message: "<checked word> is correct"". If the word is not correct then write this word first, then write the character ":" (colon), and after a single space write all its possible replacements, separated by spaces. The replacements should be written in the order of their appearance in the dictionary (in the first part of the input file). If there are no replacements for this word then the line feed should immediately follow the colon.
Sample Inputi is has have be my more contest me too if award # me aware m contest hav oo or i fi mre # #
Sample Outputme is correct aware: award m: i my me contest is correct hav: has have oo: too or: i is correct fi: i mre: more me
Transmitters2001 Mid Central Regionals
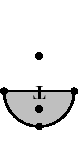
In a wireless network with multiple transmitters sending on the same frequencies, it is often a requirement that signals don't overlap, or at least that they don't conflict. One way of accomplishing this is to restrict a transmitter's coverage area. This problem uses a shielded transmitter that only broadcasts in a semicircle. A transmitter T is located somewhere on a 1,000 square meter grid. It broadcasts in a semicircular area of radius r. The transmitter may be rotated any amount, but not moved. Given N points anywhere on the grid, compute the maximum number of points that can be simultaneously reached by the transmitter's signal. Figure 1 shows the same data points with two different transmitter rotations.
All input coordinates are integers (0-1000). The radius is a positive real number greater than 0. Points on the boundary of a semicircle are considered within that semicircle. There are 1-150 unique points to examine per transmitter. No points are at the same location as the transmitter.
Input SpecificationInput consists of information for one or more independent transmitter problems. Each problem begins with one line containing the (x, y) coordinates of the transmitter followed by the broadcast radius, r. The next line contains the number of points N on the grid, followed by N sets of (x, y) coordinates, one set per line. The end of the input is signalled by a line with a negative radius; the (x, y) values will be present but indeterminate. Figures 1 and 2 represent the data in the first two example data sets below. Figures 1a and 2 show transmitter rotations that result in maximal coverage.
Output SpecificationFor each transmitter, the output contains a single line with the maximum number of points that can be contained in some semicircle.
Sample Input25 25 3.5 7 25 28 23 27 27 27 24 23 26 23 24 29 26 29 350 200 2.0 5 350 202 350 199 350 198 348 200 352 200 995 995 10.0 4 1000 1000 999 998 990 992 1000 999 100 100 -2.5
Sample Output3 4 4
|
 N
N  1) if j is the smallest number such
that the value of the j-th iterative application of the inventory function is
self-inventorying. For instance, 21221314 is self-inventorying after 2 steps, since
the
inventory of 21221314 is 31321314, the inventory of 31321314 is 31123314,
and 31123314 is self-inventorying.
1) if j is the smallest number such
that the value of the j-th iterative application of the inventory function is
self-inventorying. For instance, 21221314 is self-inventorying after 2 steps, since
the
inventory of 21221314 is 31321314, the inventory of 31321314 is 31123314,
and 31123314 is self-inventorying.