|  |
|
Czech ACM Student Chapter
CTU in Prague, Dept. of Computer Science and Engineering ÈVUT FEL++ 2003 ContestDear contestants:In two weeks, an important referendum will be held in the Czech Republic. The people will vote whether or not to enter the European Union. We do not want to give you any advices, how you should vote. There are many other people and celebrities doing that. Instead, we want you to know of some interesting behind-the-scenes details about the Union. Thus, we have prepared a set of problems that remain unsolved until today. Now, you are to write several programs to solve these problems and to help the Republic on its way to Europe. All of the programs will run in UNIX environment. Every program should read data from the standard input and send results to the standard output. The data format is given and must be exactly followed. There will be no extra spaces in the input and there should be no extra spaces and newlines in the output, if not stated otherwise. The end-of-line character is not considered a part of the line. All numbers will fit into the standard signed integer type of 32 bits, if the description of a particular problem does not say otherwise. We wish you a lot of fun and good luck with solving these problems.
Your organizing team
intro.ps
The problems have been taken from the following sources:
Booklet Printing
There are many interesting documents that are printed in the member states every day. Most of them have some restrictions regarding the format of print-outs. And some of these documents are required to be printed in the form of fold-up brochures (or booklets) instead of simple pages. When printing out a document, normally the first page is printed first, then the second, then the third, and so on until the end. However, when creating a fold-over booklet, the order of printing must be altered. A fold-over booklet has four pages per sheet, with two on the front and two on the back. When you stack all the sheets in order, then fold the booklet in half, the pages appear in the correct order as in a regular book. For example, a 4-page booklet would print on 1 sheet of paper: the front will contain page 4 then page 1, and the back will contain page 2 then page 3.
Your task is to write a program that takes as input the number of pages to be printed, then generates the printing order.
Input SpecificationThe input file contains one or more test cases, followed by a line containing the number 0 that indicates the end of the file. Each test case consists of a positive integer n on a line by itself, where n is the number of pages to be printed; n will not exceed 100.
Output SpecificationFor each test case, output a report indicating which pages should be printed on each sheet, exactly as shown in the example. If the desired number of pages does not completely fill up a sheet, then print the word `Blank'' in place of a number. If the front or back of a sheet is entirely blank, do not generate output for that side of the sheet. Output must be in ascending order by sheet, front first, then back. Print one blank line after each test case.
Sample Input1 14 4 0
Sample OutputPrinting order for 1 pages: Sheet 1, front: Blank, 1 Printing order for 14 pages: Sheet 1, front: Blank, 1 Sheet 1, back : 2, Blank Sheet 2, front: 14, 3 Sheet 2, back : 4, 13 Sheet 3, front: 12, 5 Sheet 3, back : 6, 11 Sheet 4, front: 10, 7 Sheet 4, back : 8, 9 Printing order for 4 pages: Sheet 1, front: 4, 1 Sheet 1, back : 2, 3
To Europe! To Europe!
Almost everyone in the candidate states wants to `go to Europe'', although most of the people have very vague ideas about what this actually means. Anyway, immediately after the borders are open, the inhabitants will take their cars and trucks and will `go to Europe''. This can cause many troubles, as the roads will be suddenly overloaded by vehicles of various types. You are to help to solve some of these traffic jams. Assume a convoy of vehicles has lined up in front of a single lane and one-way bridge over a river. Note that since the street is single lane, no vehicle can overtake any other. The bridge can sustain a given maximum load. To control the traffic on the bridge, operators are stationed on either end of the bridge. The convoy of vehicles is to be divided into groups, such that all the vehicles in any group can cross the bridge together. When a group reaches the other side, the operator on that side of the bridge uses a telephone to inform the operator on this side that the next group can start its journey over the bridge. The weight of each vehicle is known. The sum of the weights of the vehicles in any group cannot exceed the maximum load sustainable by the bridge. Associated with each vehicle is the maximum speed with which it can travel over the bridge. The time taken by a group of vehicles is calculated as the time taken by the slowest vehicle in the group to cross the bridge. The problem is to find the minimum amount of time in which the entire convoy can cross the bridge.
Input SpecificationThe input consists of several test cases. The first line of each test case contains three positive integers (separated by blanks): the first one represents the maximum load that the bridge can sustain b (in tonnes); the second one represents the length of the bridge l (in kms); and the third one is the number of vehicles (n) in the convoy.
Each of the next n lines of input contains a pair of
positive integers,
wi and si
(separated by blanks), where wi is the
weight of the vehicle
(in tonnes) and si is the maximum speed (in
kmph) with which this vehicle
can travel over the bridge. The weights and speeds of the vehicles are
specified in the same order as the order in which the vehicles are queued
up. You can assume that 1 After the last vehicle, the next test case description begins. The last test case is followed by a line containing three zeros.
Output SpecificationThe output of the program should be a single real number specifying the minimum time in minutes in which the convoy can cross the bridge. The number should be displayed with one digit after the decimal point.
Sample Input100 5 10 40 25 50 20 50 20 70 10 12 50 9 70 49 30 38 25 27 50 19 70 0 0 0
Sample Output75.0
Live on No Evil
One of the Czech ministers wants to run for the chair in the European Parliament. Now he is preparing his election campaign, which is based on the following simple program: that people should behave well, be nice to each other, and live on good business only. For this purpose, he needs some mottos in English language. For example, the motto he likes most is `Live on no evil'' because of its special property: it says the same thing when read backwards! Such strings are called palindromes. The minister wants to find more palindromic sentences and mottos, such as `Rats live on no evil star'', `Was it a car or a cat I saw?'', etc. You are to write a computer program which is able to detect not only palindromes but also so called mirrored strings. With that program, he can produce more great mottos and then easily win the election. A regular palindrome is a string of numbers or letters that is the same forward as backward. For example, the string "ABCDEDCBA" is a palindrome because it is the same when the string is read from left to right as when the string is read from right to left. A mirrored string is a string for which when each of the elements of the string is changed to its reverse (if it has a reverse) and the string is read backwards the result is the same as the original string. For example, the string "3AIAE" is a mirrored string because "A" and "I" are their own reverses, and "3" and "E" are each others' reverses. A mirrored palindrome is a string that meets the criteria of a regular palindrome and the criteria of a mirrored string. The string "ATOYOTA" is a mirrored palindrome because if the string is read backwards, the string is the same as the original and because if each of the characters is replaced by its reverse and the result is read backwards, the result is the same as the original string. Of course, "A", "T", "O", and "Y" are all their own reverses. A list of all valid characters and their reverses is as follows. Note that `0'' (zero) and `O'' (the letter) are considered the same character and therefore only the letter `O'' is a valid character.
Input SpecificationInput consists of strings (one per line) each of which will consist of one to twenty valid characters. There will be no invalid characters in any of the strings. Your program should read to the end of file.
Output SpecificationFor each input string, you should print the string starting in column 1 immediately followed by exactly one of the following strings:
Note that the output line is to include the dashes and spacing exactly as shown in the table above and demonstrated in the example below.
Sample InputNOTAPALINDROME ISAPALINILAPASI A3MEA ATOYOTA
Sample OutputNOTAPALINDROME -- is not a palindrome. ISAPALINILAPASI -- is a regular palindrome. A3MEA -- is a mirrored string. ATOYOTA -- is a mirrored palindrome. P.S.: You do not need to make your own program palindromic, although such programs definitely have a better aesthetic value. See below for a small example.
char rahc
[ ]
=
"\n/"
,
redivider
[ ]
=
"RATS LIVE ON NO EVIL STAR"
,
*
deliver,reviled
=
1+1
,
niam ; main
( )
{/*\}
\*/
int tni
=
0x0
,
rahctup,putchar
( )
,LACEDx0 = 0xDECAL,
rof ; for
(;(int) (tni);)
(int) (tni)
= reviled ; deliver =
redivider
;
for ((int)(tni)++,++reviled;reviled* *deliver;deliver++,++(int)(tni)) rof
=
(int) -1- (tni)
;reviled--;--deliver;
(tni) = (int)
- 0xDECAL + LACEDx0 -
rof ; for
(reviled--,(int)--(tni);(int) (tni);(int)--(tni),--deliver)
rahctup = putchar
(reviled* *deliver)
;
rahctup * putchar
((char) * (rahc))
;
/*\
{\*/}
Bodyguards
A new directive of European Union specifies exact rules for positioning bodyguards of important persons, such as presidents, government members, etc. These rules are very restrictive and must be obeyed by member states. For the purpose of the directive, an area guarded by bodyguards is considered to form a rectangular system. Each square field of the area is either empty or contains a wall. No two bodyguards can be placed onto the same horizontal row or vertical column unless there is at least one wall separating them. The goal is to place bodyguards to the area so that no two of them violate the above rule. Such position is then called legal.
Your task is to write a program that, given a description of
an area,
calculates the maximum number of bodyguards that can be placed there in
a legal configuration. The program will be a prototype only, thus,
it is
enough to restrict our attention to small square areas (at most
4 The following image shows five pictures of the same area. The first picture is the empty area, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this area, the maximum number of bodyguards in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.

Input SpecificationThe input file contains one or more area descriptions, followed by a line containing the number 0 that signals the end of the file. Each area description begins with a line containing a positive integer n that is the size of the area; n will be at most 4. The next n lines each describe one row of the area, with a dot (`.'') indicating an open space and an uppercase letter `X'' indicating a wall. There are no spaces in the input file.
Output SpecificationFor each test case, output one line containing the maximum number of bodyguards that can be placed in the area in a legal configuration.
Sample Input4 .X.. .... XX.. .... 2 XX .X 3 .X. X.X .X. 3 ... .XX .XX 4 .... .... .... .... 0
Sample Output5 1 5 2 4
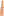 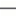   
Jugs
During the admission talks, the Czech representatives meet with other diplomats from other countries. One day, after the dinner, the diplomats started to chat very informally. Among other things, they were discussing a scene from the movie `Die Hard 3''. In that movie, Bruce Willis and Samuel L. Jackson were confronted with the following puzzle: They were given a 3-gallon jug and a 5-gallon jug and were asked to fill the 5-gallon jug with exactly 4 gallons. The Czech representatives liked that puzzle very much and decided to generalize it. You are to write a program which can solve this generalized version. Assume you have two jugs, A and B, and an infinite supply of water. There are three types of actions that you can use:
A problem is given by a triple (CA, CB, N), where CA and CB are the capacities of the jugs A and B, respectively, and N is the goal. A solution is a sequence of steps that leaves exactly N gallons in any of the jugs. The possible steps are:
Input Specification
Input to your program consists of a series of input lines each defining
one
puzzle. Input for each puzzle is a single line of three positive
integers:
CA, CB,
and N. CA and
CB are the capacities of jugs A
and
B, and N is the goal. You can assume 0 <
CA
Output SpecificationOutput from your program will consist of a series of instructions from the list of the potential actions which will result in either of the jugs containing exactly N gallons of water. The last line of output for each puzzle should be the line `success''. After that line, output one empty line to terminate the puzzle. The actions must be identified exactly as specified above. Output lines start in column 1 and there must be no empty lines and no trailing spaces. The sequence of operations found by your program has to be as short as possible, i.e., you are to find the solution which requires the minimal number of steps. If more solutions with the same number of steps exist, choose any one of them.
Sample Input3 5 4 5 7 3
Sample Outputfill B pour B A empty A pour B A fill B pour B A success fill A pour A B fill A pour A B success Please note a little special meaning of evaluation system responses for this problem. If you get a `presentation error'', it may mean your program produces unknown actions or other unrecognized lines of output. On the other hand, `wrong answer'' means your program generates a valid list of actions but they do not represent the shortest solution.
Numerically Speaking
Foreign languages are one of the main problems met by the candidate countries. The people do not have good knowledge of languages. Then, electronic translators must come to help. A developer of such devices has decided to develop a mapping between all possible words and unique integers. Such mapping can also be handy for creating crossword puzzles and other similar word games. The mapping is very simple, with the ordering being done first by the length of the word, and then alphabetically. Part of the list is shown below.
Your job in this problem is to develop a program which can translate, bidirectionally, between the unique word numbers and the corresponding words. You may assume that no word will be longer than 20 characters.
Input SpecificationInput to the program is a list of words and numbers, one per line starting in column one, followed by a line containing a single asterisk (`*'') in column one. A number will consist only of decimal digits (0 through 9) followed immediately by the end of line (that is, there will be no commas in input numbers). A word will consist of between one and twenty lowercase alphabetic characters (`a'' through `z'').
Output SpecificationThe output is to contain a single line for each word or number in the input data. This line is to contain the word starting in column one, followed by an appropriate number of blanks, and the corresponding word number starting in column 23. Word numbers that have more than three digits must be separated by commas at thousands, millions, and so forth.
Sample Input29697684282993 transcendental 28011622636823854456520 computationally zzzzzzzzzzzzzzzzzzzz *
Sample Outputelementary 29,697,684,282,993 transcendental 51,346,529,199,396,181,750 prestidigitation 28,011,622,636,823,854,456,520 computationally 232,049,592,627,851,629,097 zzzzzzzzzzzzzzzzzzzz 20,725,274,851,017,785,518,433,805,270 P.S.: As you can see, some numbers in this problem clearly will not fit into a standard integer type.
Pipe
There is a high demand in the European Union for some of traditional Czech products. One of the most requested articles is a famous `plum brandy'' (or slivovitz). To be able to satisfy the high demand, the producers decided to build a pipeline from Southern Moravia to Northern Germany, so called `slivovicovod''. The GX Light Pipeline Company started to prepare bent pipes for the new slivovitz pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.
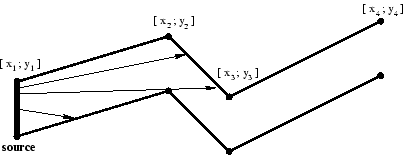
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], ..., [xn; yn], where x1 < x2 < ... xn. These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; yi-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; y1-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.
Input Specification
The input file contains several blocks each describing one pipe
component. Each block starts with the number of bent points 2
Output SpecificationThe output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message `Through all the pipe.''. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message `Through all the pipe.'' will appear in the output file.
Sample Input4 0 1 2 2 4 1 6 4 6 0 1 2 -0.6 5 -4.45 7 -5.57 12 -10.8 17 -16.55 0
Sample Output4.67 Through all the pipe.
Stock Market Ratio
When entering the European Union, the candidate countries have to get used to new business customs, especially to the stock market and its behavior. If you ever see a televised report on stock market activity, you can hear the anchorperson say something like `Gainers outnumbered losers 14 to 9,'' which means that for every 14 stocks that increased in value that day, approximately 9 other stocks declined in value. Often, as you hear that, you'll see on the screen something like this:
As a person with a head for numbers, you'll notice that the anchorperson could have said `Gainers outnumbered losers 5 to 3'', which is a more accurate approximation to what really happened. After all, the exact ratio of winners to losers is (to the nearest millionth) 1.660754, and he reported a ratio of 14 to 9, which is 1.555555, for an error of 0.105199; he could have said `5 to 3'', and introduced an error of only 1.666667 - 1.660754 = 0.005913. The estimate `5 to 3'' is not as accurate as `1498 to 902'' of course; evidently, another goal is to use small integers to express the ratio. So, why did the anchorperson say `14 to 9?'' Because his algorithm is to lop off the last two digits of each number and use those as the approximate ratio. What the anchorman needs is a list of rational approximations of increasing accuracy, so that he can pick one to read on the air. Specifically, he needs a sequence a1, a2, ..., an where a1 is a rational number with denominator 1 that most exactly matches the true ratio of winners to losers (rounding up in case of ties), ai+1 is the rational number with least denominator that provides a more accurate approximation than ai, and anis the exact ratio, expressed with the least possible denominator. Given this sequence, the anchorperson can decide which ratio gives the best tradeoff between accuracy and simplicity. For example, if 5 stocks rose in price and 4 fell, the best approximation with denominator 1 is 1/1; that is, for every stock that fell, about one rose. This answer differs from the exact answer by 0.25 (1.0 vs 1.25). The best approximations with two in the denominator are 2/2 and 3/2, but neither is an improvement on the ratio 1/1, so neither would be considered. The best approximation with three in the denominator 4/3, is more accurate than any seen so far, so it is one that should be reported. Finally, of course, 5/4 is exactly the ratio, and so it is the last number reported in the sequence. Can you automate this process and help the anchorpeople?
Input SpecificationThe input file contains several pairs of positive integers. Each pair is on a line by itself, beginning in the first column and with a space between the two numbers. The first number of a pair is the number of gaining stocks for the day, and the second number is the number of losing stocks for the day. The total number of stocks never exceeds 5000.
Output SpecificationFor each input pair, the standard output should contain a series of approximations to the ratio of gainers to losers. The first approximation has 1 as denominator, and the last is exactly the ratio of gainers to losers, expressed as a fraction with least possible denominator. The approximations in between are increasingly accurate and have increasing denominators, as described above. If there are two approximations with the same denominator, which are equally accurate, choose the one with a higher numerator. The approximations for a pair are printed one to a line, beginning in column one, with the numerator and denominator of an approximation separated by a slash (`/''). A blank line follows each sequence of approximations.
Sample Input5 4 1498 902
Sample Output1/1 4/3 5/4 2/1 3/2 5/3 48/29 53/32 58/35 63/38 68/41 73/44 78/47 83/50 88/53 93/56 377/227 470/283 563/339 656/395 749/451 P.S.: Please keep in mind that if your program produces more approximation pairs than needed, you will probably get the `presentation error'' response, although the `wrong answer'' would be more appropriate in that case.
Spreadsheet
In 1979, Dan Bricklin and Bob Frankston wrote VisiCalc, the first spreadsheet application. It became a huge success and, at that time, was the killer application for the Apple II computers. Today, spreadsheets are found on most desktop computers. And, with the admission to the European Union, their importance even raises. There are important computations to be performed by businessmen. For instance, they may want to determine, whether it is better to buy a Czech product or some of its variants made in other countries. The idea behind spreadsheets is very simple, though powerful. A spreadsheet consists of a table where each cell contains either a number or a formula. A formula can compute an expression that depends on the values of other cells. Text and graphics can be added for presentation purposes. You are to write a very simple spreadsheet application. Your program should accept several spreadsheets. Each cell of the spreadsheet contains either a numeric value (integers only) or a formula, which only support sums. After having computed the values of all formulas, your program should output the resulting spreadsheet where all formulas have been replaced by their value.
Input SpecificationThe first line of the input file contains the number of spreadsheets to follow. A spreadsheet starts with a line consisting of two integer numbers, separated by a space, giving the number of columns and rows. None of these numbers will not exceed 1000. The following lines of the spreadsheet each contain a row. A row consists of the cells of that row, separated by a single space. A cell consists either of a numeric integer value or of a formula. A formula starts with an equal sign (`=''). After that, one or more cell names follow, separated by plus signs (`+''). The value of such a formula is the sum of all values found in the referenced cells. These cells may again contain a formula. There are no spaces within a formula. You may safely assume that there are no cyclic dependencies between cells. So each spreadsheet can be fully computed. The name of a cell consists of one to three letters for the column followed by a number between 1 and 999 (including) for the row. The letters for the column form the following series: A, B, C, ..., Z, AA, AB, AC, ..., AZ, BA, ..., BZ, CA, ... ZZ, AAA, AAB, AAC, ... AAZ, ABA, ..., ABZ, ACA, ..., ALK. These letters correspond to the numbers from 1 to 999. The top left cell has the name A1. See the figure above.
Output SpecificationThe output of your program should have the same format as the input, except that the number of spreadsheets and the number of columns and rows are not repeated. Furthermore, you should print one blank after each spreadsheet to terminate it. And, of course, all formulas must be replaced by their values.
Sample Input1 4 3 10 34 37 =A1+B1+C1 40 17 34 =A2+B2+C2 =A1+A2 =B1+B2 =C1+C2 =D1+D2
Sample Output10 34 37 81 40 17 34 91 50 51 71 172 P.S.: Note that we do not require asymptotically optimal solution to this problem. All large test cases are randomly generated and they do not contain any specially designed patterns.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 n,b,l,s
n,b,l,s  i
i  [1..n]: wi
[1..n]: wi  4 fields).
4 fields).