|  |
|
České vysoké učení technické a Univerzita Karlova
Katedra počítačů FEL ČVUT, Czech ACM Chapter, Kabinet software a výuky informatiky MFF UK, ve spolupraci s Katedrou informatiky FEI VŠB-TU Ostrava CTU Open Contest 2001V dnešním světě plném techniky je třeba vzdělaných lidí. Potvrzuje to i studie Dr.Ozda Singa z Číny, která odhaluje i překvapivou skutečnost, že nadání k přírodním vědám a matematice obvzlášť se projevuje již ve velmi raném věku. Matematicky nadané malé dítě se brzy dovtípí, že když jste koupili dvě lízátka a ono snědlo jen jedno, tak to druhé přeci někde musí být. Skutečnost, že druhé lízátko již dávno zkonzumoval sourozenec, pak je už jen zanedbatelnou odchylkou reality od teorie. Matematicko-fyzikální fakulta se rozhodla podporovat takto nadané děti již od raného věku (zajistí si tím mimo jiné i stálý přísun studentů) a založila matfyzáckou školku. Pro školku byla vybrána budova MFF na Malé Straně, která právě nyní prochází rekonstrukcí. Vás si MFF vybrala, abyste jí pomohli s řešením některých náročnějších problémů, které se při přestavbě budovy na školku či při vybavování školky objevily. Při psaní vašich programů je především důležitá rychlost (profesoři i projektanti jsou přeci jen dost netrpěliví) a paměť je až na druhém místě. Všechny programy, které máte vytvořit, mají číst vstupní data ze standardního vstupu a výsledky vypisovat na standardní výstup. V obou případech je třeba přesně dodržet předepsaný formát. Je-li vstupem více hodnot na jednom řádku a není-li uvedeno jinak, jsou hodnoty odděleny právě jednou mezerou. Vstup ani výstup neobsahuje žádné přebytečné mezery, není-li v zadání úlohy uvedeno jinak. Pokud se v zadání vyskytují celá čísla a není u příslušné úlohy řečeno jinak, tak je velikost čísel vždy volena tak, aby se všechna tato čísla i případné výsledky vešly do standardního typu int v C či integer v Pascalu. Hodně štěstí při řešení úloh! Vaši organizátoři
    ![]](poc-right.gif)
Komunikace
Při výchově malých matfyzáčků je třeba dbát i na vzájemnou komunikaci. Proto
je nezbytné, aby každé dvě místnosti v matfyzácké školce byly propojeny
počítačovou sítí. Pro účely této úlohy si budovu školky budeme představovat jako
kvádr mající V pater, kde v každém patře je R
Specifikace Vstupu
Vstup se skládá z několika bloků. Každý blok popisuje budovu, pro
kterou je úlohu třeba vyřešit. Blok začíná trojicí čísel V, R, S
na prvním řádku, 1
Specifikace VýstupuVýstup má obsahovat pro každou budovu jeden řádek s textem: "Budova je jiz dostatecne propojena.", pokud jsou všechny místnosti v budově již propojeny sítí, nebo text "Ocekavana cena: XXXX Kc", kde "XXXX" značí minimální cenu, která je potřeba k propojení všech místností sítí. Při výpisu ceny je třeba oddělit trojice číslic uskupené dle jejich řádu čárkou způsobem obvyklým v anglosaských zemích (viz vzorový výstup).
Vzorový vstup3 2 2 *-* |.. *-* o.o ... o.o *.* ..| *.* ... ... ... *-* |.. *.* 2 2 2 *-* |.. *.* ..o ... o.o *-* ... *-* 0 0 0
Vzorový výstupOcekavana cena: 3,000 Kc Budova je jiz dostatecne propojena.
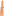 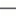  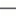 ![]](poc-right.gif)
SměrniceRekonstrukce malostranské budovy Matematicko-fyzikální fakulty si vyžádá značné množství finančních prostředků. Jen financování programátorů, kteří pracují na zefektivnění práce dělníků, si vyžádá nemalé peníze na bagety, Coca-colu a personál, který dohlíží na udržování základních životních funkcí těchto pracovníků. Raději zde ani nebudeme zmiňovat náklady na platy skupiny kontrolující efektivitu práce programátorů. Proto byla vydána směrnice děkana SM2001/364 o kontrole pohybu finančních prostředků. Tato směrnice například určuje, který pracovník má oprávnění uvolnit peníze na maltu, který na cihly a který na okna. Směrnice dále přísně nařizuje archivaci a střežení veškerých údajů o výdajích fakulty, specifikuje způsob zápisu jednotlivých nabídek od dodavatelů a postup, jak pro potřeby fakulty vybírat dodavatele a případně i jejich subdodavatele.
Pro ilustraci si představme, že fakulta dostala nabídky od padesáti firem. Každá firma potřebuje pro výrobu svého produktu (případně svých produktů) nějaké suroviny, které jí mohou dodat některé jiné firmy. Přirozeně cena výsledných produktů závisí na cenách surovin, ze kterých je produkt vyráběn. Nyní je fakulta postavena před problém, jak získat některé suroviny co nejlevněji.
Kromě problémů spojených s rekonstrukcí budovy je také potřeba řešit financování běžného chodu fakulty. Každá katedra získává kromě prostředků z celofakultního rozpočtu také prostředky z grantů, od sponzorů apod. Tyto peníze pak katedry utrácejí mimo jiné za nákup nového hardwaru a softwaru. Celý systém financování je tedy potřeba zpřehlednit, a proto bylo rozhodnuto vytvořit jednotný fakultní finanční software pod vedením komise, která byla pro tento účel jmenována děkanem.
Když byl tento problém předložen analytikům placeným fakultou, tito se zděsili a odmítli úlohu jako neřešitelnou. Proto se nadřízená komise rozhodla, že od implementace této části nařízení zatím upustí a nechá naimplementovat alespoň část směrnice upravující správu fakultních kont.
Směrnice říká, že veškeré operace s konty musí projít přes speciální fakultní program, který všechny informace zaznamená a odhalí případné nesrovnalosti. Naimplementovat tento program je právě úkol pro vás.
Specifikace VstupuProgram na vstupu dostane několik řádků. Na každém řádku je zapsána jedna operace v bance. Operace mohou být následující:
účet je desetimístné číslo účtu. částka je číslo s právě dvěma místy za desetinnou tečkou. V jednom okamžiku má fakulta v bance nejvýše 10 000 účtů. Operace ZALOZ vytvoří nový účet s číslem účet. Operace ULOZ uloží na účet účet částku částka. Operace VYBER vybere z účtu účet částku částka. Operace PREVED převede částku částka z účtu účet1 na účet účet2. Operace STATISTIKA a LIST pouze vypíší informace o účtech v bance. Operace RESET zruší všechny existující účty a uvede systém do počátečního stavu.
Specifikace VýstupuNa výstup má operace ZALOZ vypsat řádek "Ucet účet vytvoren.". Pokud účet účet již existuje, má se na výstup vypsat text "Ucet účet uz existuje.". Operace ULOZ má vypsat řádek "Ulozeno částka na ucet účet.". Pokud účet účet neexistuje, má se vypsat "Ucet účet neexistuje.". Operace VYBER má vypsat řádek "Vybrano částka z uctu účet.". Pokud účet neexistuje, má se vypsat "Ucet účet neexistuje.". Pokud na účtu není dostatek peněz, má se vypsat text "Nedostatek penez.". Operace PREVED má vypsat "Prevedeno částka z uctu účet1 na ucet účet2.", pokud je vše vpořádku. Pokud neexistuje účet účet1, je třeba vypsat řádek s textem "Ucet účet1 neexistuje.". Pokud existuje účet1, ale není na něm dost peněz, je třeba vypsat zprávu "Nedostatek penez.". Pokud neexistuje účet účet2, je třeba ke všem předchozím zprávám vypsat text "Ucet účet2 neexistuje.". Operace STATISTIKA má vypsat text "Pocet uctu: XXXX", kde XXXX je počet účtů existujících v bance. Na dalším řádku pak text "Celkem: YYYY", kde YYYY je součet peněz na všech účtech dohromady. Součet peněz je třeba vypsat tak, že celá část součtu bude vypsána na sedm míst a zarovnaná doprava. Pak bude následovat desetinná tečka a desetinná část součtu vypsaná na právě dvě místa. Operace LIST má vypsat text "Pocet uctu: XXXX", kde XXXX je počet účtů v bance. Na dalších řádcích pak následují řádky obsahující informace o jednotlivých účtech. Na každém řádku je informace o jednom účtu, pořadí účtů ve výpisu je takové, v jakém byly účty zakládány. Pro každý účet je vypsán text ve tvaru "účet částka", kde celá část čísla částka je vypsána na sedm míst a zarovnaná doprava, desetinná část čísla je vypsána na právě dvě místa. Po výpisech všech účtů je třeba vypsat řádek s textem "Celkem: YYYY", kde YYYY je součet peněz na všech účtech. Celou část součtu je třeba vypsat na sedm míst zarovnanou doprava, desetinnou část na právě dvě místa. Operace RESET má vypsat zprávu "Reset systemu.". Po provedení všech operací má program vypsat na samostatný řádek text "Konec.". Mezi zprávy od dvou operacích je třeba vždy vložit prázdný řádek.
Vzorový vstupZALOZ 0000000001 ULOZ 0000000001 2.00 VYBER 0000000001 1.00 STATISTIKA RESET ZALOZ 1000000001 ULOZ 1000000001 20.50 ZALOZ 1000000002 PREVED 1000000001 1000000002 15.25 ZALOZ 1000000002 VYBER 1000000002 14.00 VYBER 1000000002 10.00 LIST
Vzorový výstupUcet 0000000001 vytvoren. Ulozeno 2.00 na ucet 0000000001. Vybrano 1.00 z uctu 0000000001. Pocet uctu: 1 Celkem: 1.00 Reset systemu. Ucet 1000000001 vytvoren. Ulozeno 20.50 na ucet 1000000001. Ucet 1000000002 vytvoren. Prevedeno 15.25 z uctu 1000000001 na ucet 1000000002. Ucet 1000000002 uz existuje. Vybrano 14.00 z uctu 1000000002. Nedostatek penez. Pocet uctu: 2 1000000001 5.25 1000000002 1.25 Celkem: 6.50 Konec.
    ![]](poc-right.gif)
Matematické cvičeníMalí matfyzáčci se musí odmala cvičit v matematice. Protože ale látka jako řešení soustav diferenciálních rovnic či integrace ve vícerozměrných prostorech je pro ně ještě příliš obtížná, je potřeba vyučovat něco jednoduššího. Po dlouhých debatách se rozhodlo, že se bude vyučovat prosté sčítání; ovšem v různých soustavách. Vaším úkolem bude napsat program, který bude žáčky kontrolovat.
Specifikace VstupuNa vstupu je několik bloků. Každý blok mimo posledního začíná řádkem s kladným celým číslem z, z 35, poslední blok začíná nulou a
nemá být zpracováván. Na druhém řádku každého bloku se nachází
dvě nezáporná čísla x a y oddělená mezerou, která jsou
zapsána standardním způsobem
v soustavě o základu z. U soustav o základu větším než 10 se pro
cifry s hodnotou větší než 9 používá písmen A, B....
Pokud má soustava základ jedna, používá se pouze cifra jedna a
a počet cifer je roven velikosti čísla (viz vzorový výstup);
nula se v jedničkové soustavě zapisuje jako jednociferné číslo,
jehož jediná cifra 0. Čísla, která váš program obdrží na vstupu,
nebudou na svém začátku obsahovat přebytečné nuly.
Čísla mají nejvýše 1 000 cifer. 35, poslední blok začíná nulou a
nemá být zpracováván. Na druhém řádku každého bloku se nachází
dvě nezáporná čísla x a y oddělená mezerou, která jsou
zapsána standardním způsobem
v soustavě o základu z. U soustav o základu větším než 10 se pro
cifry s hodnotou větší než 9 používá písmen A, B....
Pokud má soustava základ jedna, používá se pouze cifra jedna a
a počet cifer je roven velikosti čísla (viz vzorový výstup);
nula se v jedničkové soustavě zapisuje jako jednociferné číslo,
jehož jediná cifra 0. Čísla, která váš program obdrží na vstupu,
nebudou na svém začátku obsahovat přebytečné nuly.
Čísla mají nejvýše 1 000 cifer.
Specifikace VýstupuVýstup má obsahovat pro každý blok na vstupu jeden řádek. Na řádku mají být vypsána čísla x a y oddělená mezerou, znakem + a mezerou. Za nimi má následovat mezera, znak =, mezera a číslo x+y. Všechna čísla mají být zapsána standardním způsobem v soustavě o základu z.
Vzorový vstup16 A0 FE 1 1111 11 0
Vzorový výstupA0 + FE = 19E 1111 + 11 = 111111
    ![]](poc-right.gif)
ČervotočiDo stolů ve školce se pustili červotoči a začali v nich vyhlodávat chodbičky. Aby bylo možno správně nadávkovat ochranný prostředek, je třeba zjistit, kolik dřeva již sežral nejžravější červotoč (když by totiž červotoč sežral příliš velkou dávku ochranného prostředku, mohl by zmutovat a stát se ještě nebezpečnějším). Protože každý červotoč má charakteristický způsob tunelování, můžeme snadno zjistit, kterou chodbičku vyhlodal který červotoč.
Specifikace Vstupu
Vstup se skládá z několika bloků. Každý blok vyjma posledního začíná třemi čísly R, S a C,
kde 1
Specifikace VýstupuNa výstup má váš program pro každý blok na vstupu vypsat text "Nejzravejsi cervotoc je XXXX.", kde XXXX bude nahrazeno jménem červotoče, který sežral nejvíce částí stolu. Můžete předpokládat, že takovýto červotoč bude určen jednoznačně.
Vzorový vstup4 10 2 Adam Bohus **A***BBB* *A**AAA*B* **AA***BBB ****AA**** 0 0 0
Vzorový výstupNejzravejsi cervotoc je Adam.
    ![]](poc-right.gif)
Algebra
Malí matfyzáčci mají obvykle problém s algebraickými strukturami.
Proto si budou ve školce procvičovat operace s permutacemi. Aby
ale cvičení mělo smysl a matfyzáčci se něco naučili, byla zadefinována
netradiční operace, tzv. trojúhelníková operace. Trojúhelníková operace
má tři parametry i, j a k. i
Specifikace VstupuVstup se skládá z několika bloků. Každý blok začíná řádkem s počtem prvků v permutaci N, 3 N N  100 000. Vstup je ukončen řádkem obsahujícím
nulu. Tento řádek nemáte dále zpracovávat.
Na druhém řádku každého bloku je N vesměs různých celých čísel z intervalu
1 až N, která popisují cílovou permutaci. 100 000. Vstup je ukončen řádkem obsahujícím
nulu. Tento řádek nemáte dále zpracovávat.
Na druhém řádku každého bloku je N vesměs různých celých čísel z intervalu
1 až N, která popisují cílovou permutaci.
Specifikace VýstupuNa výstup má váš program pro každý blok vypsat jeden řádek obsahující text "Permutaci lze prevest.", pokud zadanou permutaci lze získat z identické permutace pomocí posloupnosti trojúhelníkových operací. Pokud permutaci získat nelze, má řádek obsahovat text "Matfyzacci maji smulu.".
Vzorový vstup3 1 2 3 3 1 3 2 3 2 3 1 0
Vzorový výstupPermutaci lze prevest. Matfyzacci maji smulu. Permutaci lze prevest.
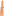 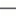  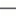 ![]](poc-right.gif)
Přeprava materiáluPři přestavbě malostranské budovy na školku je třeba převézt mnoho materiálu z jednoho místa na druhé. Převáží se například cement, písek nebo ocelové pruty, ale i poněkud křehčí zboží, jako například lavice, okna nebo počítače. Podle typu nákladu je samozřejmě třeba zvolit správný typ automobilu. A protože nafta je v dnešní době velmi drahá, je třeba také projet s automobilem co nejkratší možnou cestou. Ačkoliv systém silnic není přehnaně hustý, je dosti komplikované se v něm vyznat, a tak se fakulta rozhodla, že si nechá napsat program, který jí pomůže při rozvrhování tras pro jednotlivé náklady.
Specifikace VstupuNa vstupu je několik bloků pro jednotlivé náklady. Každý blok začíná řádkem se čtyřmi čísly N, M, S a C, kde N je počet významných míst v síti silnic (1 N N  10 000),
M je počet silnic (M 10 000),
M je počet silnic (M  50 000),
které mezi významnými místy vedou, S je číslo významného
místa (místa číslujeme od jedné do N), odkud je náklad vezen,
a C je číslo místa, kam se má náklad dopravit. Vstup je ukončen
řádkem obsahujícím čtyři nuly. Tento řádek nemáte dále zpracovávat.
Pak v bloku následuje M řádků popisující jednotlivé cesty mezi
místy. Každý z řádků obsahuje tři celá čísla A, B a V oddělená
mezerou. A je číslo místa, odkud vede silnice, B je číslo místa,
kam vede silnice (silnice jsou jednosměrné), a V jsou náklady
na přepravu materiálu po této silnici (1 50 000),
které mezi významnými místy vedou, S je číslo významného
místa (místa číslujeme od jedné do N), odkud je náklad vezen,
a C je číslo místa, kam se má náklad dopravit. Vstup je ukončen
řádkem obsahujícím čtyři nuly. Tento řádek nemáte dále zpracovávat.
Pak v bloku následuje M řádků popisující jednotlivé cesty mezi
místy. Každý z řádků obsahuje tři celá čísla A, B a V oddělená
mezerou. A je číslo místa, odkud vede silnice, B je číslo místa,
kam vede silnice (silnice jsou jednosměrné), a V jsou náklady
na přepravu materiálu po této silnici (1  V V  1 000).
Můžete předpokládat, že cesta mezi počátečním a cílovým místem vždy
existuje. 1 000).
Můžete předpokládat, že cesta mezi počátečním a cílovým místem vždy
existuje.
Specifikace VýstupuPro každý blok na vstupu na výstup vypište jeden řádek obsahující minimální cenu, za kterou lze přepravit náklad z místa S do místa C.
Vzorový vstup4 6 1 2 1 2 10 1 3 2 3 2 5 1 4 4 4 2 1 3 4 1 0 0 0 0
Vzorový výstup4
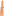    ![]](poc-right.gif)
Dámy
Malí matfyzáčci si samozřejmě musí i hrát. Proto je potřeba pro ně vytvořit
i nějaké inteligentní hry. Jednou z her, kterou budou malí matfyzáčci
hrát, je i hra na královny. Hra se hraje na toroidu N
Specifikace VstupuNa vstupu je několik řádků. Každý řádek obsahuje kladné číslo N, velikost hracího plánu. Poslední řádek obsahuje nulu. Tento řádek nemáte dále zpracovávat.
Specifikace VýstupuNa výstup máte pro každý řádek vypsat buď "Kralovny lze umistit.", pokud dámy lze umístit, nebo "Kralovny se nevejdou.", pokud dámy umístit nelze.
Vzorový vstup3 5 0
Vzorový výstupKralovny se nevejdou. Kralovny lze umistit.
    ![]](poc-right.gif)
NástěnkyVe školce je samozřejmě třeba dbát i na jistou estetickou úroveň. Proto bylo rozhodnuto, že jedna ze zdí školky bude ozdobena obrázky. V soutěži, která byla na výzdobu vypsána, se sešlo velmi mnoho návrhů (dokonce několik miniatur a jedno panorama). Nakonec byl jako vítězné dílo vybrán cyklus obrazů ,,Dějiny matematiky''. Nyní je potřeba rozhodnout o umístění tohoto výtvarného díla. K tomu je nutné vědět, jak velkou plochu musí cyklus obrazů zabírat -- tedy do jakého nejmenšího (co do obsahu) obdélníku lze obrazy umístit. Před svým vystavením budou všechny obrazy orámovány (pro jednoduchost si představujme, že šířka a výška rámu bude jeden bod). Při umísťování obrazů na stěnu je třeba zachovat jejich pořadí vzhledem k běžnému způsobu čtení textu (po řádcích zleva doprava). Celou situaci však ještě navíc komplikuje Anička Zrzavá, učitelka výtvarné výchovy pro informatiky: Obrazy je potřeba na stěnu umístit tak, aby splňovaly její náročné estetické požadavky. Stěna bude (pomyslně) rozdělena do několika vodorovných pásů, do kterých budou obrazy umístěny -- obrazy umístěné do jednoho z pásů nezasahují do žádného jiného pásu a to ani svým rámem. V rámci jednoho pásu jsou obrazy umístěny těsně vedle sebe (jejich rámy se právě překrývají). Jednotlivé obrazy mají být vycentrovány v rámci pásu svisle (pokud jsou dvě možné pozice, zvolte tu vyšší z nich) a celý úsek obrazů umístěný do pásu má být vycentrován na střed obdélníku (jsou-li dvě možnosti jejich umístění, zvolte to levější). Pokud je v rámci obdélníku stejných rozměrů více možností, jak lze obrazy rozdělit do pásů, je třeba zvolit takové jejich rozdělení, aby první pás obsahoval co nejvíce obrazů; pokud je stále více možných způsobů rozdělení obrazů, je třeba maximalizovat počet obrazů v druhém pásu atd. Pokud je více obdélníků se stejným obsahem ale různými rozměry, které jsou optimální, zvolte nejširší z nich.
Specifikace Vstupu
Vstup programu se skládá z několika bloků. Každý blok vyjma posledního
začíná řádkem s jedním číslem N (počtem obrazů v cyklu), 1
Specifikace VýstupuNa výstup má váš program pro každý blok na vstupu vypsat výšku, šířku a obsah nejmenšího nejestetičtějšího umístění obrazů. Dále je třeba na výstup toto umístění vykreslit. Obrazy je třeba vykreslovat s rámy ze znaků +, - a | s obsahem zadaným na vstupu (doplněným o chybějící mezery). Při vykreslování hran dvou horizontálně se překrývajících rámů je třeba vykreslit + v obou rozích obou rámů. Výstupy pro jednotlivá zadání jsou na výstupu odděleny jedním prázdným řádkem. Pro přehlednost vypište na začátek a na konec každého řádku obsahujícího umístění obrázků znak :; tento znak se nezapočítává do velikosti stěny. Pokud bude umístění špatně vykresleno, výsledkem vyhodnocení bude Presentation error, nikoliv Wrong answer.
Vzorový vstup2 2 3 AbC aBc 1 5 12345 4 1 10 1234567890 5 5 ABCDE BCDEA CDEAB DEABC EABCD 1 4 1 5 abcd 0
Vzorový výstup4 11 44 :+---+-----+: :|AbC|12345|: :|aBc+-----+: :+---+ : 13 12 156 :+----------+: :|1234567890|: :+----------+: :+-----+ : :|ABCDE| : :|BCDEA+----+: :|CDEAB| |: :|DEABC+----+: :|EABCD| : :+-----+ : : +-----+ : : |abcd | : : +-----+ :
|
 S místností. Jednotlivé
místnosti je samozřejmě nutné propojit s co nejmenšími náklady. Propojení dvou
sousedních místností (tzn. majících společnou stěnu) na stejném patře stojí
1000 Kč, propojení dvou místností nad sebou (tzn. strop jedné místnosti je
podlahou druhé) stojí 2000 Kč. Situaci navíc komplikuje to, že některé
místnosti již jsou propojené. Vaším úkolem je vytvořit program, který spočte
minimální náklady nutné na dopropojování místností.
S místností. Jednotlivé
místnosti je samozřejmě nutné propojit s co nejmenšími náklady. Propojení dvou
sousedních místností (tzn. majících společnou stěnu) na stejném patře stojí
1000 Kč, propojení dvou místností nad sebou (tzn. strop jedné místnosti je
podlahou druhé) stojí 2000 Kč. Situaci navíc komplikuje to, že některé
místnosti již jsou propojené. Vaším úkolem je vytvořit program, který spočte
minimální náklady nutné na dopropojování místností.
 R-1 řádek, na každé řádce je
2
R-1 řádek, na každé řádce je
2 j, j
j, j